割り算をしたとき、その数は分母と分子のどっちに行くか覚えよう! はてなブックマークやツイッター等で拡散していただけると、非常にウレシイです! ! こんばんは、なかなか記事が書けない管理人です。 本日は5÷3のような〇÷ の問題をやってみましょう。 今回の計算は下の解説のように、2通りの解き方があります。 1つ目は、「割る数を逆数にしてかける どの分数も分子が13で等しくなっています。 分子が同じ大きさの分数は、分母が大きい数ほどその分数は小さくなります。 逆に考えると分母の大きさが小さくなるほど、大きくなるということになります。 つまり、この問題の答えは、\ (\frac {13} {2},\frac割られる数が大きい場合の割り算(筆算っぽい方法) 割られる数が整数型に収まりきらない場合、割り算の筆算と同様の方法が便利な場合があります。 例えば、X、Yが正の整数として、X * Pを、Yで割る場合を考えます。結果は、32bitに必ず収まるものとします。
1
分母が大きい割り算
分母が大きい割り算-「一般に,nを1つの自然数とするとき,分母がnである有理数は等間隔 n 1 で数直 線状に並びます。nが限りなく大きくなると,この間隔は限りなく大きくなる。この ことから, 数直線状にどんなに短い線分ABをとっても,分数には3種類の呼び名があります。 1 3 真分数(しんぶんすう) 分子が分母より少さい分数 4 3 仮分数(かぶんすう) 分子が分母より大きい分数 2 1 3 帯分数(たいぶんすう) 整数と真分数の和から成る分数 ※ 2 1 3 = 2 1 3 帯分数を仮分数に




新版 なぜ分数の割り算はひっくり返すのか 数学ギライも図に描けばすぐ理解できる 板橋 悟 本 通販 Amazon
以下の左辺のように、分母より分子の方が大きい分数を仮分数といいます。 \begin{align*} \frac{9876}{54} = 1 \frac{48}{54} \end{align*} 仮分数を整数部分と小数部分に分解したものは、以下の右辺のように帯分数と呼ばれる $$ 記号を省略した書き方をすることがあり大きい数の割り算 筆算2桁の数÷1桁の数 筆算小数点以下の桁数が異なる;整数用の割り算 IP の LPM_DIVIDE を応用して、下記の方法で対応することができます。 入力の被除数(分子)を 17bit 左シフト(右に 0 を17bit 加えて 34bit)します。 除数(分母)はそのまま、34bit 数 ÷ 17bit 数 を LPM_DIVIDE で計算します。 結果(商)の 34bit 数の小数点位置を最下位ビットの右から 17bit 左
分子と分母が同等量(即ち1)か、分子が分母より大きい分数である 例として、 4 / 3 8 / 5 16 / 9 といった分数に該当する 真分数は整数ではないが、仮分数は整数でないとは限らない 例えば 2 / 1 6 / 3 48 / 12 などは整数だが、仮 第 6 回のテーマは「 分数の概念と計算方法 」です。 割り算 , 割合 , 比の「 変形 」である「 分数 」についての話です。 今までの「 割り算 , 割合 , 比 」の知識 は、この「 分数 」を理解することで 全てが繋がり、完成します 。 分数は小数とも密接な関わりがあります。 ~割り算の特性~ ①割り算っていうのは 割られる数 と 割る数 を同じ数字で かけたり割ったりしても答えは同じなので簡単にします ②割り算の答え=割られる数(分子)/割る数(分母) まず①の性質を使います ÷284 →÷2→ 44÷142 →÷2→ 22÷71 となります たぶん割り切れないはずなので ②の性質を使い分数で答えます つまり答えは 22(分子)/71(分母) になるはずです
分母が大きい分数の計算 1/81 1/108 1/162 これらを通分したいです。 分母が大きいため工夫が必要なのはわかるのですが、 どうしたらいいのかわかりません。 9の倍数ですよね、共通す る数が分母なのでしょうか。 ご教授お願いします。 ・仮分数(分子が分母より大きい分数)と、整数の割り算をします。 ・ 分数を整数で割る計算は 、下の例のように 分母に整数を掛ける ことで、計算ができます。 $$\Large\frac{3}{5}\div{2}=\frac{3}{5×2}=\frac{3}{10}$$割り算 筆算2桁の数÷2桁の数 帯分数を含む引き算(分母が同じ)



分数のかけ算のやり方 小学校5年生 大人の学び直し算数 計算のやり方解説 無料



割り算の筆算の方法 大人の学び直し算数 計算のやり方解説 無料
(2) $\dfrac{2}{5}$ は分母が分子より大きいので真分数です。 $1\dfrac{2}{3}$ は左に数字がくっついているので帯分数です。 $\dfrac{7}{4}$ は分子が分母以上なので仮分数です。 もっと詳しく:真分数、仮分数、帯分数の意味と例題 同様に、 01 × 01 = 01 ÷ 10 = × なら、「 01 を 10個に分けたときの 1 個 ( 10個で 01 になる) 」なので「 001 , 」となります。 また、1 × 10 = 1 ÷ 01 = 1 ÷ という関係でもあります。 具体的な計算の仕方は「 整数に直して計算し、最後に小数点の計算 」をします。 例えば、 25 × 15 なら「 25 × 01 × 15 × 01 」と整数を作って計算します。 25 × 15 × 01 × 01 = 375 × 001 = 3751An 1B'nn tan −1 xB'nn C ※この形の不定積分を関数として表すためには逆三角関数を必要とするため,高校では扱われないのが普通.ただし,同じ形でも 定積分 は数値の差=定数となるから,この形の定積分は高校の範囲に入る. (16) 分母が数種類の2
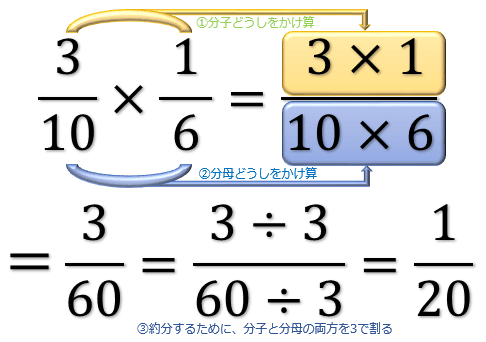



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ




帯分数 仮分数 真分数とは 足し算や引き算など計算のやり方を わかりやすく解説
・分子が同じとき,分母が大きい 倍になることを数直線上 分数の方が大きさが小さいこと で気づかせ,理解させる。 を知る。 6 ・4/5+3/5の計算の仕方を考え 同分母の真分数や仮分数の加減 真分数の加法計算におい る。 計算の仕方を,単位分数の何こ て分数のわり算 ①分数÷整数 ・真分数を整数でわるときは,分子はそのままで,分母にその整数をかけます。 ②約 分 ・約分できるときには,計算のとちゅうで約分すると,計算が簡単になります。 ③分数÷分数 ・分数を分数でわる計算は,わる数の分母と分子を入れかえた分数をかけて計算しルートの中の数が大きくなってきたときは整理していく、というルールがあります。 ルートの割り算を計算しているときに、割り切れず分数にすることがあります。 このように、分母にルートが残ったとき、分母のルートを外す作業を「有理化」といい




ルートの掛け算のうまいやり方 の中はすぐに計算しない方がいい 中学や高校の数学の計算問題
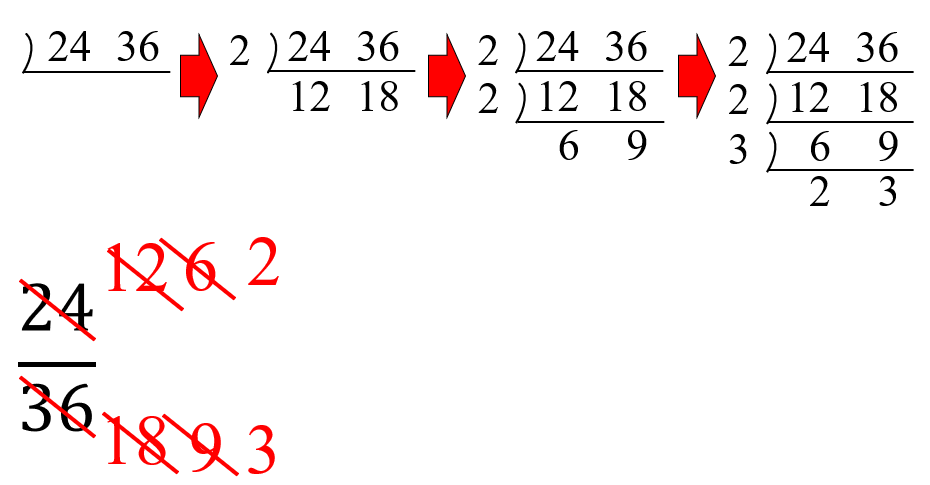



分数の約分のやり方と教え方のコツ 時間短縮に便利なテクニックを紹介 数学fun
分母が同じ分数のたし算では,分母はそのままにして,分子だけを たします。 分子だけをたす 答えの分子が分母 答えの分子と分母が より大きくなって 同じであるときは, もよい。 分数の大きさは1に したがって, なる。したがって, 分母はそのまま になる。分母の最小公倍数を見つけ、両辺にかけます。 例 =16 最小公倍数の見つけ方 150,150×2=300,150×3=450,というように大きい方の数の倍数を計算し,小さい方の数 60 でわり切れるか確認していきます。 分数のわり算、なぜ「ひっくり返す」の? 筋の通った説明、あります 2/3 ←「線」にも名前があるんです 横山 明日希 プロフィール ここまで




平方根分野の難所 掛け算と割り算をていねいに あんず学習塾のメモ 図表置き場




分数の割り算をする方法 12 ステップ 画像あり Wikihow
私の解釈がおかしいのでしょうか。 チラシに書かれた商品に興味をもつ人の割合が一定(10%)である場合、チラシの枚数との興味を持つ人の関係を式で表すと (100÷1)×01=10人 (1000÷1)×01=100人 となり、増えるのは分母ではなく分子です。 「売上目標を達成するには分母を大きくする必要がある」という言い方はチラシの枚数を分母、興味を持つ人の数を分子 分数の計算プリント全12種約3000問無料 解説&回答つき 18/1/26 分数, 計算プリント 無料で使える分数の計算プリント(ドリル)です。 足し算・引き算・掛け算・割り算の問題があります。 真分数や帯分数、分母が同じ・違うなど12種類に First Previous 1 2 分数のわり算を扱うときには「包含除」で考えることが理解するうえでの近道となります。分数のわり算は、以下のように計算しますね。 4 ÷ 2 5




何で分数の割り算は逆数をかけるの 理由を説明できますか




分数と小数 Wolfram Alphaを使って数学を勉強しよう
B:整数や小数を,分母が1,10,1000などの分数で表すことが分かる。 A:上記に加え,(小数→分数)や(整数→分数)の表し方が説明できる。 6 分数には,分母,分子がちがう,大きさの等しい分数があることを理解する。小学5年生の算数 わり算と分数|商分数/分数の第二義 練習問題プリント 分数にある2つの意味のうち、第一義 ( 1を3等分したものを2つ集めたもの= 2/3 )は3年生で学習します。 このページのプリントでは、第二義 ( 2を3でわったもの= 2/3 )つまり、わり算の商を表すための分数 (商の分数)を中心に、その表し方や計算方法を練習します。 (プリント10枚) 基本的に 分母の次数は分子の次数よりも小さくすることを心がけましょう 。なぜなら もし分母の方が大きいなら割り算が必ずできるはず ですから。 整式同士の割り算はこの記事で解説して




分数と小数 Wolfram Alphaを使って数学を勉強しよう



1
ただし分母と分子の差が大きい時、あまりこのテクニックは有用ではありません。 \(\dfrac {21}{49}=\dfrac {3}{7}\)⇒\((4921=28)\) この例だと分母分子の差\(28\)は分子\(21\)よりも大きく 魔法のルール②からは、分数がわり算であることもわかります。 \(\large\sf{\frac{2}{3}}\)→2を3等分したもの→2÷3 つまり、 「÷」の前の数字が分子(わられる数)、後の数字が分母(わる数) です。大きい数の割り算 筆算2桁の数÷1桁の数 筆算2桁の数÷1桁の数(商の1の位0) 筆算2桁の数÷1桁の数(商の10の位0) 筆算3桁の数÷1桁の数;




今さら聞けない 大きい数字 分数 掛け算 割り算 色々な数の読み方 英語が苦手でも聴いてtoeic900点




平方根分野の難所 掛け算と割り算をていねいに あんず学習塾のメモ 図表置き場
割り算には、「割られる数」と「割る数」があります。 「1÷2」で「1」が「割られる数」、「2」が「割る数」です。 割り算を分数で表すと1/2ですが、分子が「割られる数」、分母が「割る数」です。 今回は割られる数と割る数の意味、関係、商と余り、見分け方について説明します。 分数、分子と分母の詳細は、下記が参考になります。 分数とは? 1分でわかる




温度が の空気で水蒸気が1 2g含まれている時の湿度を小数点第2位を四捨五入して Clear




帯分数 仮分数 真分数とは 足し算や引き算など計算のやり方を わかりやすく解説



分母とは 1分でわかる意味 分子 有理化 マイナス 0 分母が大きい 小さい



1



割り算の筆算の方法を教えてください 例 284この様に小さい数を Yahoo 知恵袋



分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料




小学4年生 算数 無料問題集一覧 おかわりドリル




分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ




鹿浜地域学習センター 鹿浜図書館 この夏 勉強を頑張りたい小学生の皆さんへ 鹿浜地域学習センターオリジナルの算数プリントを配信します 今回は初級編として 足し算と引き算 低学年向け 掛け算と割り算 中学年向け 分数の種類と考え方



割り算の筆算の方法 大人の学び直し算数 計算のやり方解説 無料
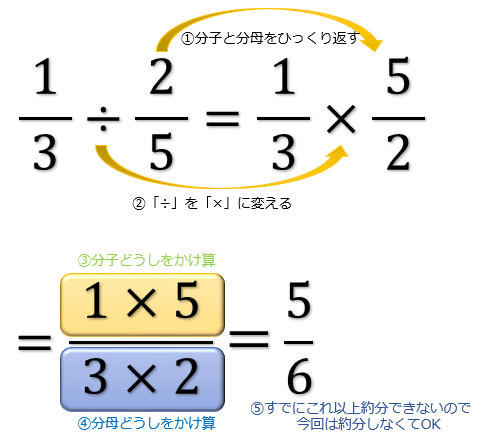



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ



分数の問題です 14 50や 45 300のように 小さい数字を大きい数 Yahoo 知恵袋
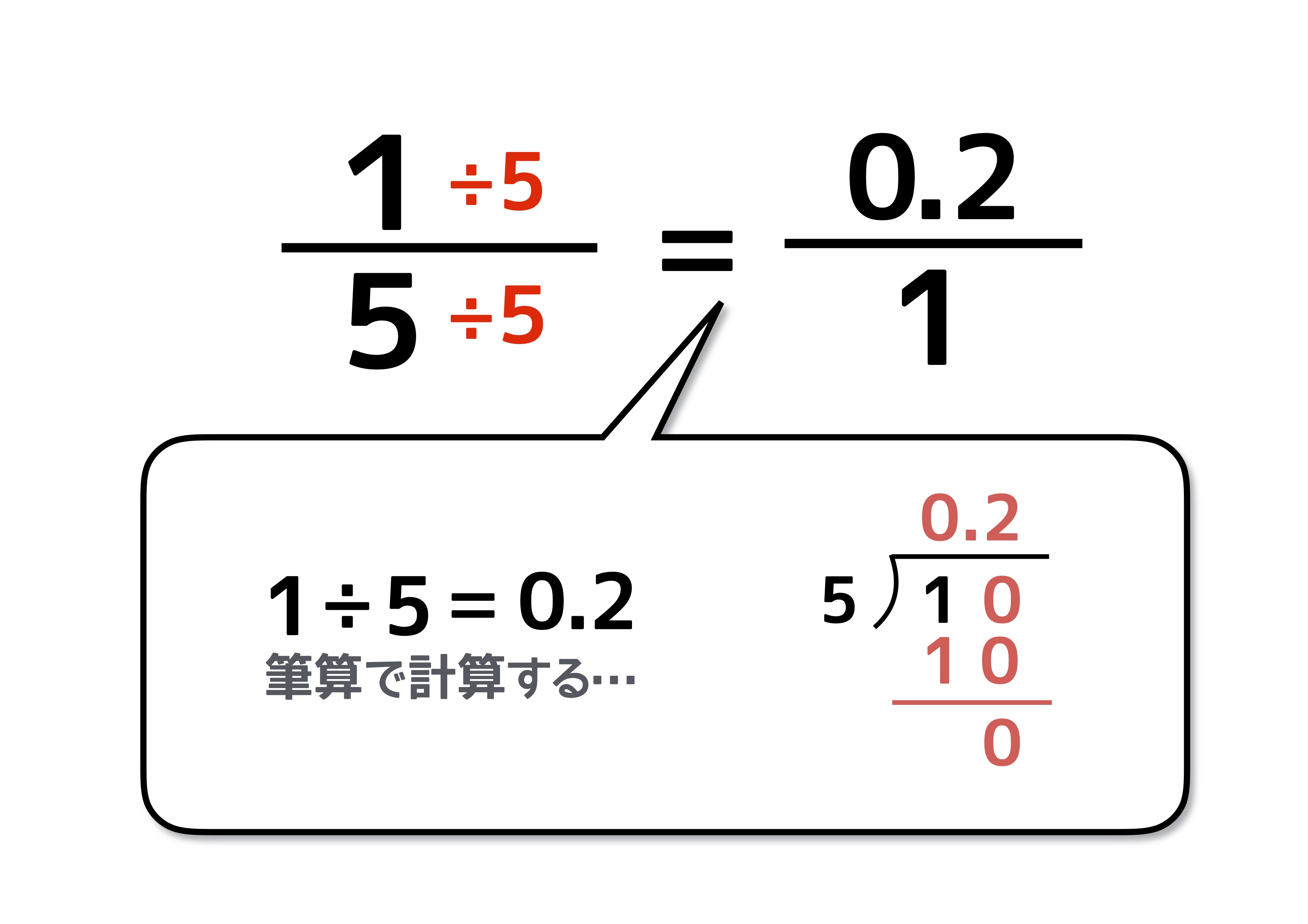



分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ




通分の新着記事 アメーバブログ アメブロ




高校数学 分数式の加法と減法 分子の次数下げ 受験の月




割るってなあに 303 Books



割り算の筆算の方法 大人の学び直し算数 計算のやり方解説 無料



誤答から学ぼうシリーズ 相加平均と相乗平均の関係 その4 ほのぼの数学頑張ろう



分数のわり算



分数のかけ算のやり方 小学校5年生 大人の学び直し算数 計算のやり方解説 無料



分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料
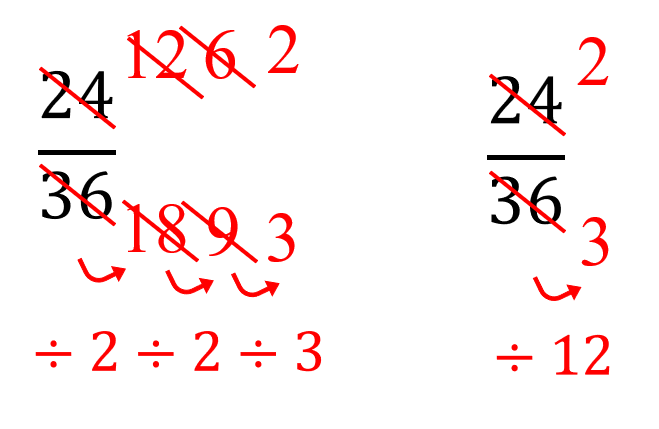



分数の約分のやり方と教え方のコツ 時間短縮に便利なテクニックを紹介 数学fun




小学4年生 算数問題プリント集です 計算プリント Com 1 6年生小学校 算数問題 無料ドリルプリント集
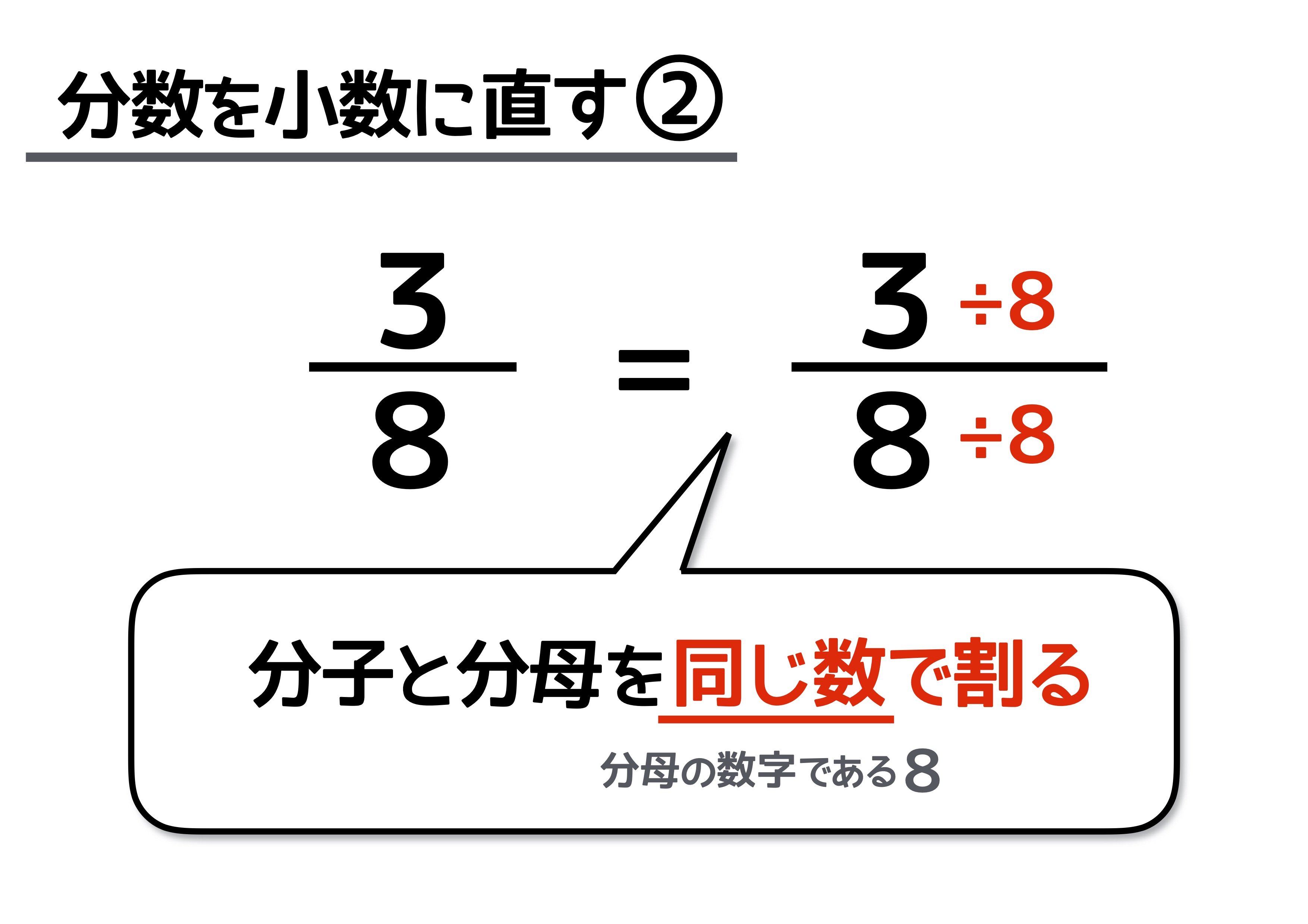



分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ




帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun




なぜ分数の割り算はひっくり返すのか お試し版




多項式の次数の求め方 一番大きい次数を答えるだけだ 中学や高校の数学の計算問題



1



割り算の筆算の方法を教えてください 例 284この様に小さい数を Yahoo 知恵袋
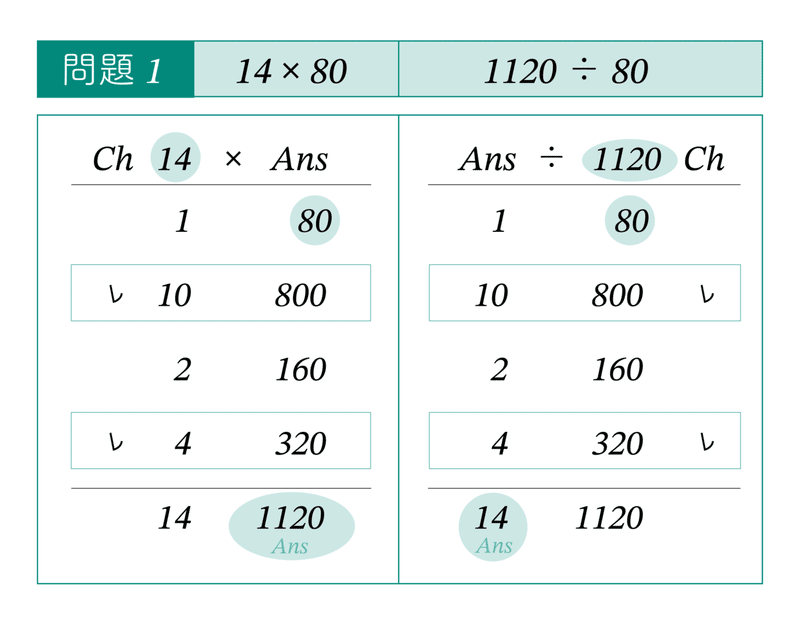



エジプト分数の割り算 Part1 拡張規則を使った計算 ラッセル博士の数のお話 Note




大きい数のわり算 小学生無料算数学習プリント 無料プリントのぷりんと365




数基礎 Com 分数の各部の名称が分かる方法




小学4年生 算数 無料問題集 分母が同じ帯分数の引き算 おかわりドリル




複数桁の小数で割り算 ビデオ 小数の割り算 カーンアカデミー




分数 の英語 3 13などの読み方と正しく伝わる簡単テクニック




この計算式 ややこしいです 間違わずにスムーズに解きたいんですが 計算式 Clear




何 割り算で解答0って リフォーム Diy 整備の自由人



割り算の筆算の方法を教えてください 例 284この様に小さい数を Yahoo 知恵袋




小学校5年算数 小数 小数5 1より小さい数で割る Mathlab Youtube
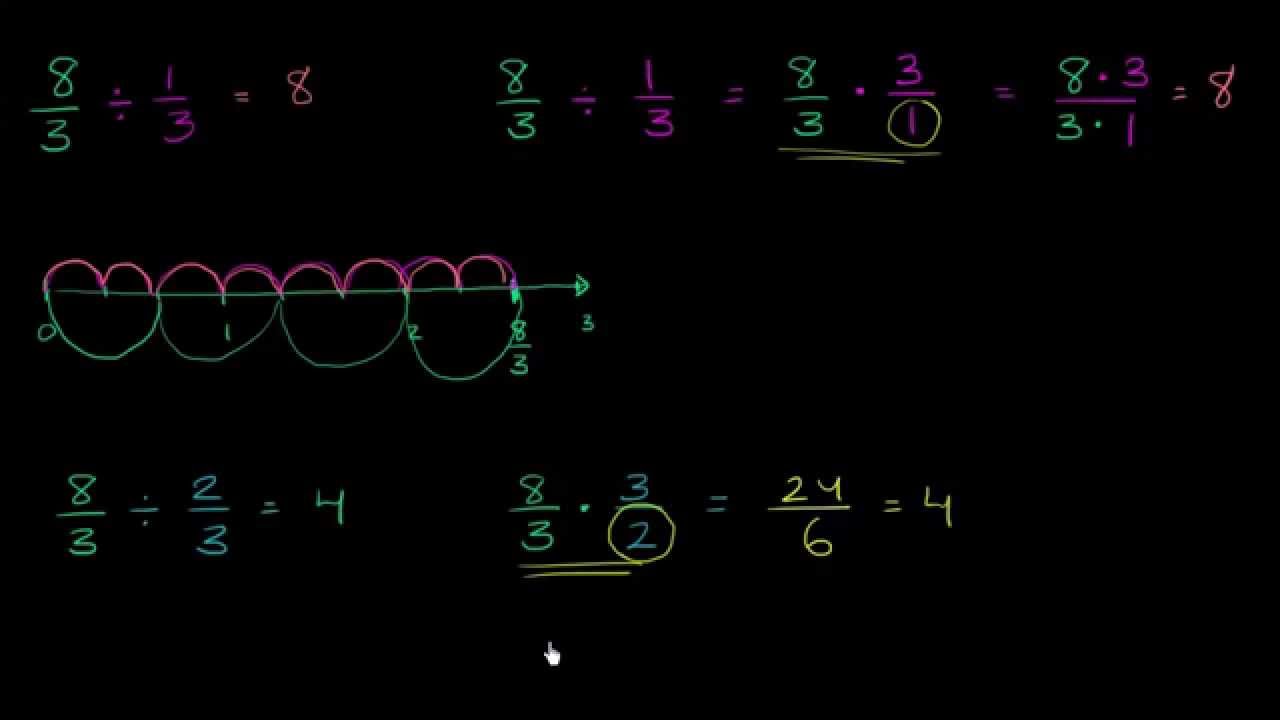



分数どうしの割り算を理解する ビデオ 分数を分数で割る カーンアカデミー




平方根分野の難所 掛け算と割り算をていねいに あんず学習塾のメモ 図表置き場




小学4年生 算数問題プリント集です 計算プリント Com 1 6年生小学校 算数問題 無料ドリルプリント集




分数の割り算 花鳥風月の風流を楽しんでる暇もない




小3 算数 小3 26 大きい数のわり算 Youtube
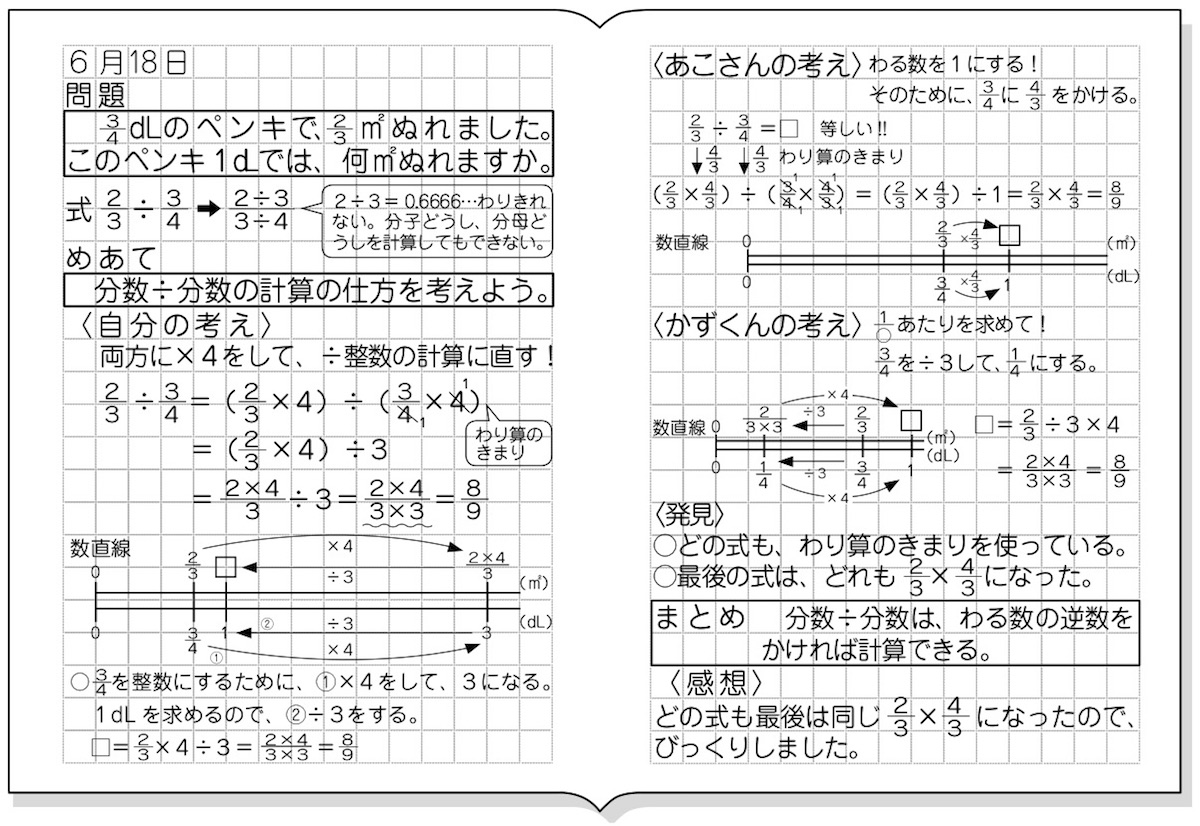



小6算数 分数のわり算 指導アイデア みんなの教育技術
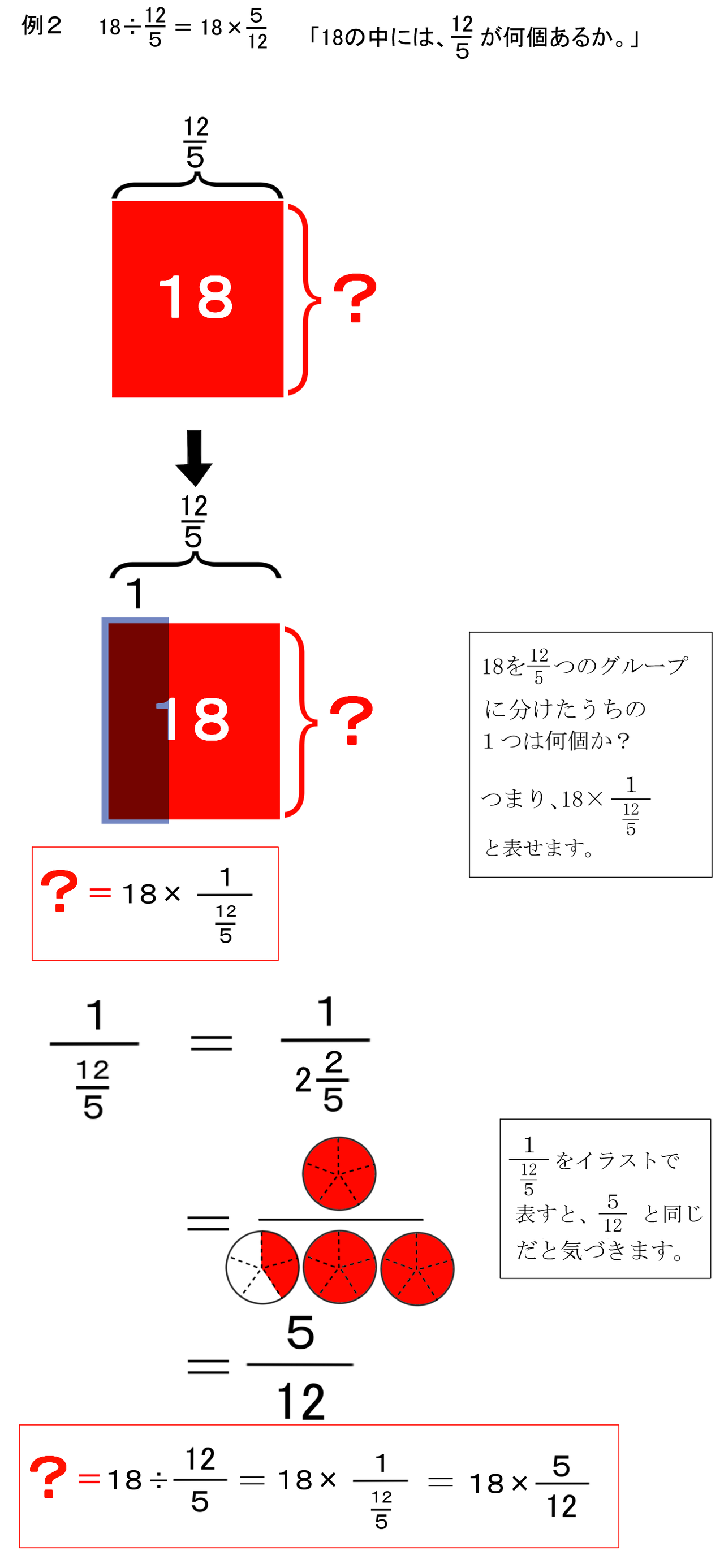



疑問1 なぜ分数の割り算では 分子と分母を逆にするの バカでもわかる 中学数学




帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun



割り算の筆算 小学レベル で質問なのですが 左と右とでやっている操作 答え Yahoo 知恵袋



割られる数と割る数は 1分でわかる意味 関係 商と余り 見分け方




小学4年生の算数 筆算 割り算 3桁 2桁の計算 商のたつ位に気をつけよう 練習問題プリント ちびむすドリル 小学生




小学生向け 算数 プリント 答えが二桁となる割り算 学習塾 Step By Step



割り算の筆算の方法 大人の学び直し算数 計算のやり方解説 無料




数学ゾンビだ 分数の約分の問題は完璧に解ける息子さん 意味を理解しないまま計算してたことがわかった時の話 Togetter




平方根分野の難所 掛け算と割り算をていねいに あんず学習塾のメモ 図表置き場




1999 号 計算装置及び計算処理プログラムが記憶された記憶媒体 Astamuse




分数 まなび365 小学生の算数プリントを自動作成 無料で自宅学習




分数の割り算の考え方と解き方 なぜ割る数を逆数にしてかけるか Cocoiro ココイロ Part 5



分母が違って 数が大きい同士の分数のかけ算のやり方を教えて下さい Yahoo 知恵袋




分数の割り算は なぜ分子と分母をひっくり返して掛ければよい のか 創造とコミュニケーションの実践




小学生向け 算数 プリント 答えが二桁となる割り算 学習塾 Step By Step




C でプロジェクトオイラーを解く 問題33 桁消去分数 みつおの雑記ブログ
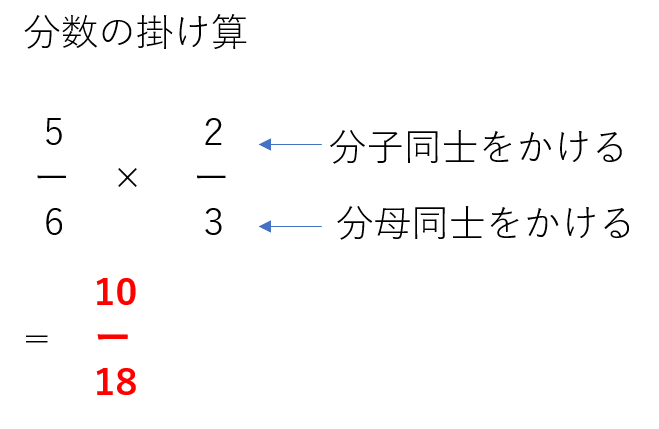



小学生に 分数 の教える時の5つのコツは 絶対に親が知っておきたい内容はこれ




どうやつてするのですか わかる人教えてください お願いします Clear




分数の大小関係 通分や小数にするのが解き方のコツだ 中学や高校の数学の計算問題




小学生に 分数 の教える時の5つのコツは 絶対に親が知っておきたい内容はこれ



分数の問題です 14 50や 45 300のように 小さい数字を大きい数 Yahoo 知恵袋




割り算をしたとき その数は分母と分子のどっちに行くか覚えよう 中学や高校の数学の計算問題




世界と戦うための英語力 を身につける 神田外語extension




分数の割り算の考え方と解き方 なぜ割る数を逆数にしてかけるか Cocoiro ココイロ Part 5
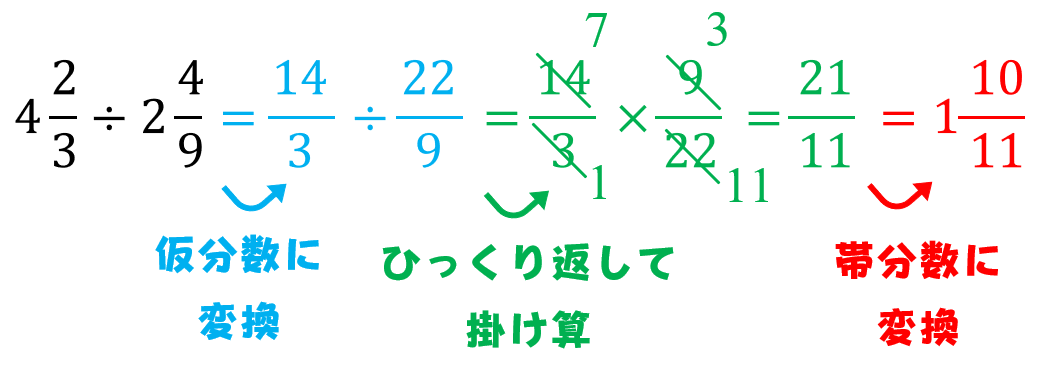



帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun




分数と小数の比べ方 直し方 変換 教え方 計算方法 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服




新版 なぜ分数の割り算はひっくり返すのか 数学ギライも図に描けばすぐ理解できる 板橋 悟 本 通販 Amazon




小学生に 分数 の教える時の5つのコツは 絶対に親が知っておきたい内容はこれ




小6 算数 小6 8 分数のわり算 Youtube



分数の問題です 分母が大きい分数の計算はどのように計算すればやりや Yahoo 知恵袋



割り算の筆算の方法を教えてください 例 284この様に小さい数を Yahoo 知恵袋




大きい数でも約分したい ユークリッドの互除法 すうがくブログ 式変形ch
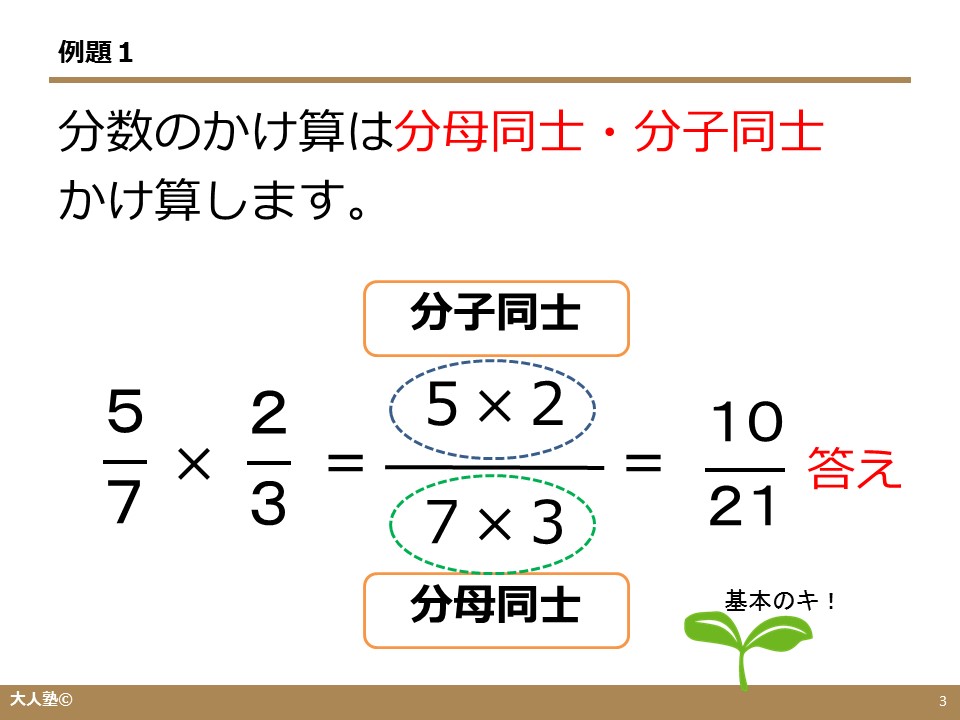



分数のかけ算のやり方 小学校5年生 大人の学び直し算数 計算のやり方解説 無料



Www Junten Ed Jp Contents Wp Content Uploads 13 04 5e2729f9f865bf9fa53d15f4fa9246 Pdf




数学 これから 約分 の話をしよう
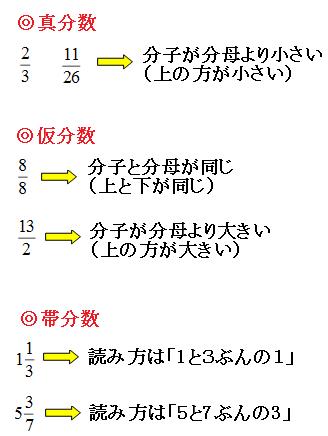



分数の基本をわかりやすく解説 分数とは何か を意識できれば超便利




温度が の空気で水蒸気が1 2g含まれている時の湿度を小数点第2位を四捨五入して Clear
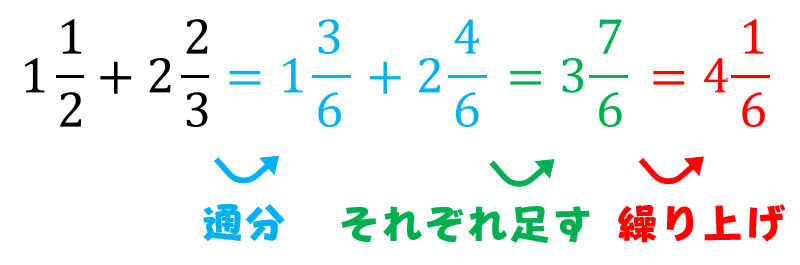



帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun
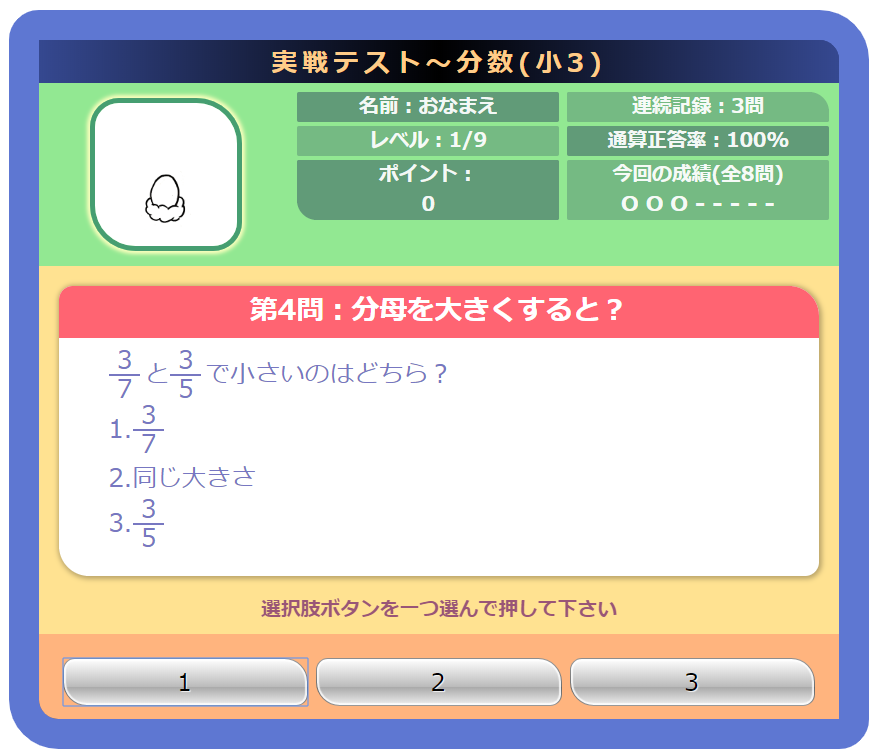



小学3年生で習う分数は 分数の意味 数直線など そうちゃ式 分かりやすい図解算数 別館
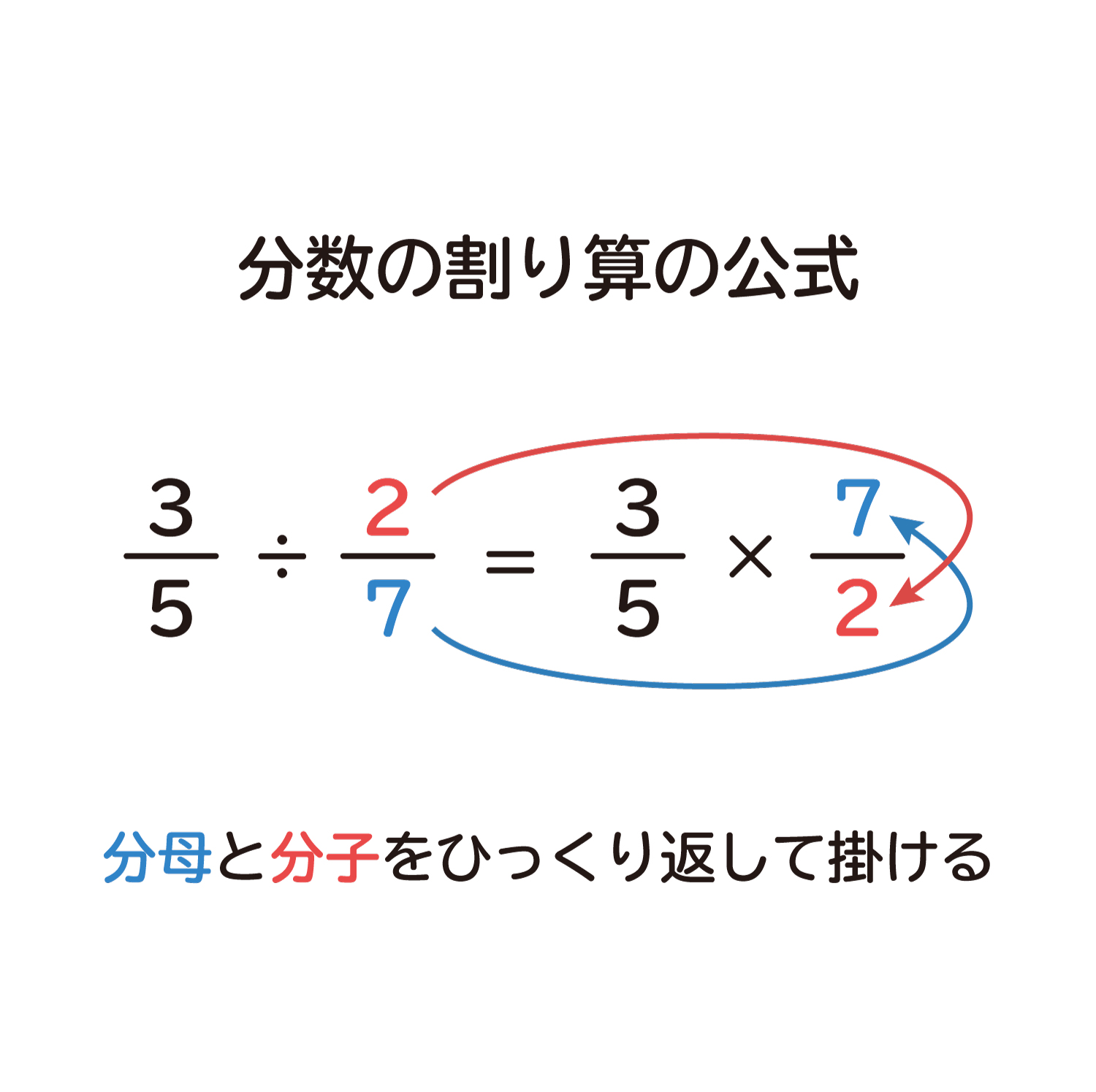



なぜ 分数の割り算は分母と分子をひっくり返して掛ける のか を説明します おかわりドリル



小さい数を大きい数で割る割り算が分かりません 10 7 12 1とか小数点 Yahoo 知恵袋




分数の約分のやり方と教え方のコツ 時間短縮に便利なテクニックを紹介 数学fun



1




エジプト分数の割り算 Part1 拡張規則を使った計算 ラッセル博士の数のお話 Note
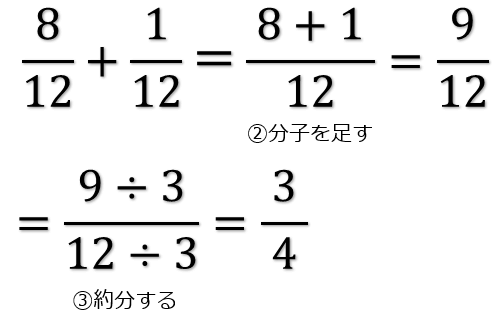



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ



0 件のコメント:
コメントを投稿