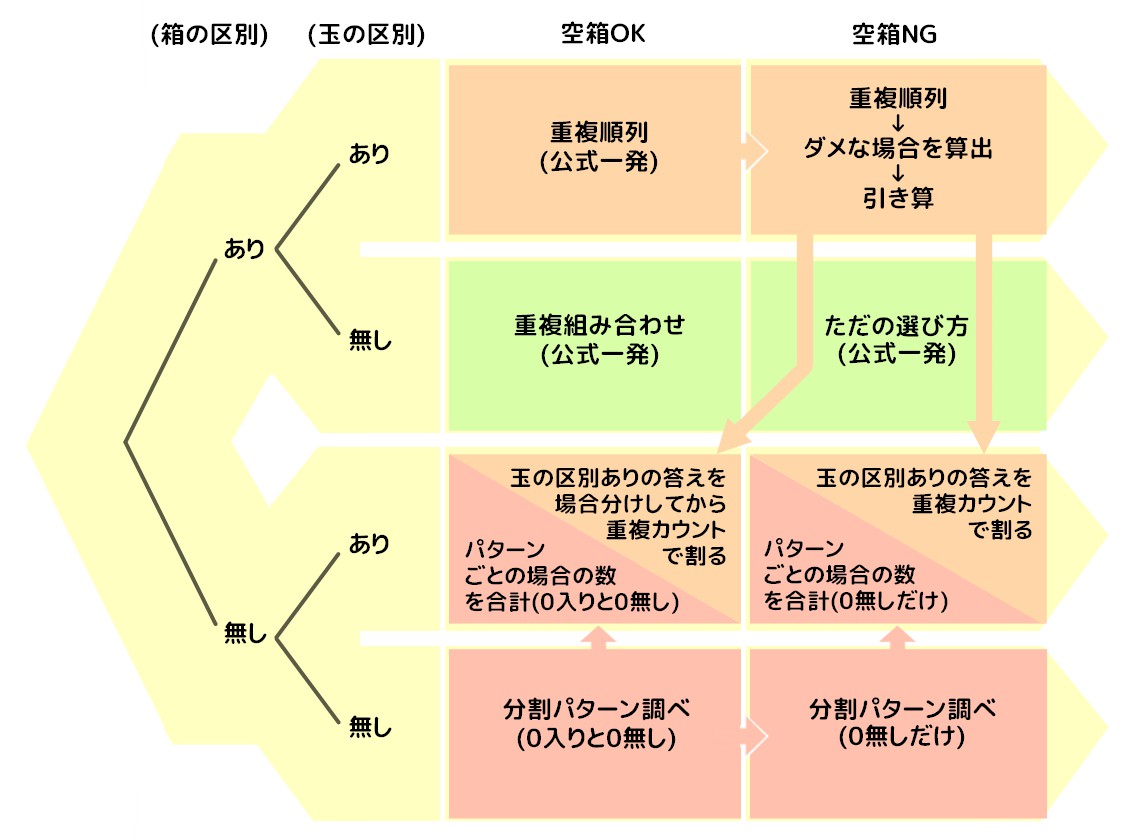
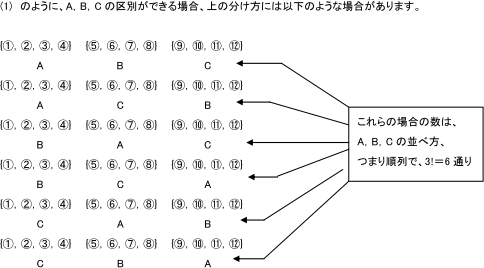
場合の数分野では,\ 断りがない限り,\ 人は区別できると考える よって,\ は{「モノの区別可」「組の区別可」「要素の個数固定」}型である これは,\ 組分けの中で最も基本的で単純な型である a君,\ b君,\ c君に,\ 順に3個ずつ{選}{ん}{で}分ける}と考える} まず,\ a}君に分ける3個の選び方は,\ 9個見分け方まとめ:順列、組合せ、円、重複、組分けの違い 順列、組み合わせ、円、重複、組分け。 これらの場合の数の違いとその見分け方を簡単に解説します。 ここでは共通の例として、7個のガラス玉があった場合を考えてみます。 重複組合せとしてと同様に考えるには,\ 0以上である必要がある 1以上の場合,\ \ 2本が連続することが許されない そこで,\ {0以上となるように変数変換を行う} y,\ zも同様に変換し,\ X,\ Y,\ Zのみの式にすると,\ と同じ問題に帰着する {x,\ y,\ zとX,\ Y,\ Zは1対1に対応する}から,\ X,\ Y,\ Zの組

高校数学a 組合せの活用1 点を結ぶ 例題編 映像授業のtry It トライイット
場合の数 組み合わせ 公式
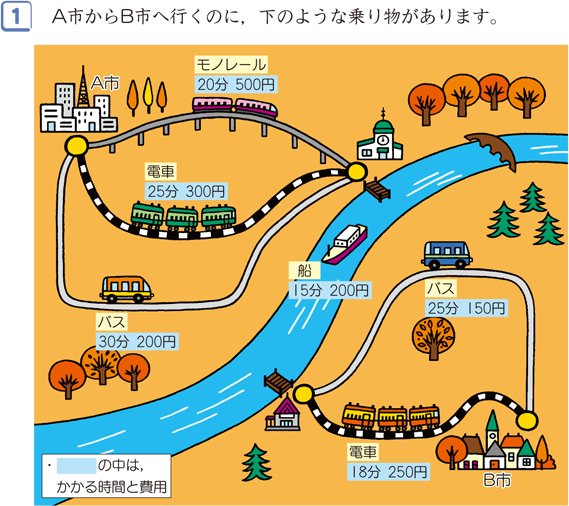
場合の数 組み合わせ 公式-組合せ場合の数において、最重要の「組合せ」練習問題を通じて、理解を深めましょう。例題1\(6\) 人を、\(a,b\) の \(2\) つの部屋に分ける。次の問いに答えなさい。(1)\(a\) に \(4\) 人、\(b\) に \(2\) 人となる分け方は全部で何通りありますか。(2) \(6\) 人の分け方は全部で何通りありますか両端指定,整数の順列 → 印刷用PDF版は別頁 両端が男子である並び方 例1 男子3人,女子2人の合計5人が1列に並ぶとき,両端が男子であるような並び方は何通りあるか <考え方> 両端に制限がついているときは,はじめに両端から並べると考え




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート
場合の数(組合せ)を求める計算では、分母と分子でかけ算をする前に、先に約分をしてしまうのがコツです。 これが分子の「6」と約分できます。 かけ算のケアレスミスを防ぐためにも 約分は必ず先に しましょう。 答え.35通り ツルカメ算、旅人算、流水算など特殊算の解説動画が充実 組合せ :「選ぶだけで並べない」「ABとBA 47 47 47 都道府県から 5 5 5 つ選ぶ場合の数 はいくつあるか。 解答 (1) 順番を区別しないので組合せで, 5 C 2 = 10 {}_5\mathrm{C}_2=10 5 C 2 = 10 通り。 (2) リーダーと副リーダーは別物なので順列で, 5 P 2 = {}_5\mathrm{P}_2= 5 P 2 = 通り。 (3) 例えば 123 123 123例えば,2人の人a,bに同質のお菓子3個を分ける方法の数を数えたいものとする.ただし,どちらかが1つももらわない場合や全部もらってしまう分け方も許されるものとする. {a,a,a} {a,a,b} {a,b,b} {b,b,b} これは,異なる2人の名前を重複を許して3回呼ぶ場合の数に等しい.(名前が呼ばれたらお菓
これは、この組み合わせの数の公式を使う事で 5C2=5×4÷2=10通り と求めることができます。 下のように表にして考えると「並びだけが違う、組み合わせとして見たら同じものが1セットにつき 2! =2 個ずつ存在する」のが分かりやすくなります。 「1× m となります。 よってお客様の声 アンケート投稿 よくある質問 リンク方法 組合せ 110 /92件 表示件数 1 1140 30歳代 / 自営業 / 非常に役に立った / 使用目的 ゲームの
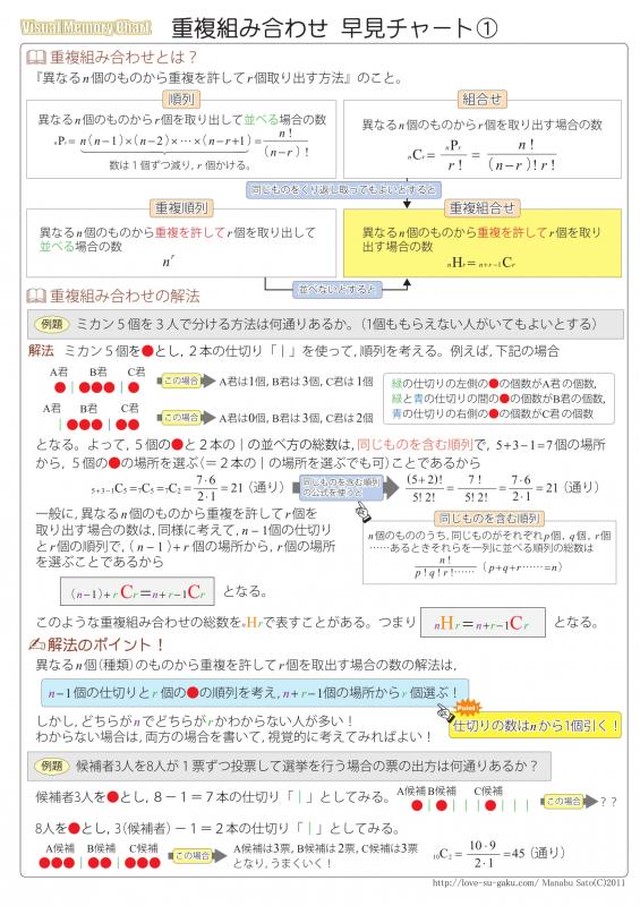
重複組合せの公式を使う 実は,重複組合せは以下の公式で計算できます。 n n n 種類のものから重複を許して r r r 個選ぶ場合の数は n r − 1 C r {}_ {nr1}\mathrm {C}_r nr−1 さて,この問題を重複組合せの考え方で解いてみましょう. 8 8 個の と, 2 2 本の仕切り を適当に一列に並べると,そのひとつの並び方が上の問題のひとつの整数解の組に対応します. よって,求める整数解の個数は 10C2 = 45 10 C 2 = 45 通りです.つまり(2) n C r = n P r r!




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



Q Tbn And9gcqk 07pns6gblxpztbesi Hjq Rmi0dl3bcobqphecjrlms6b O Usqp Cau
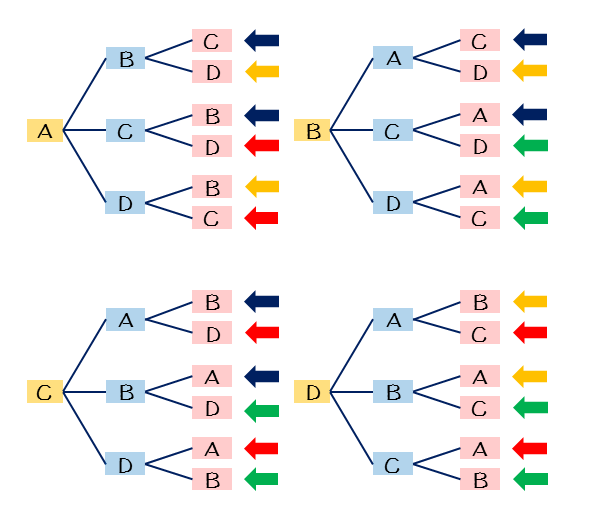
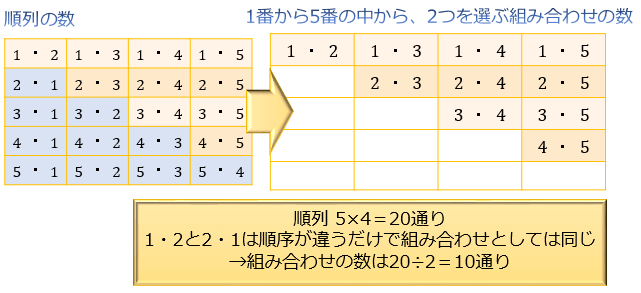
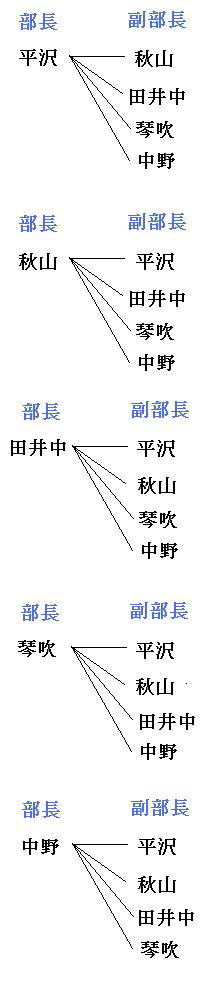
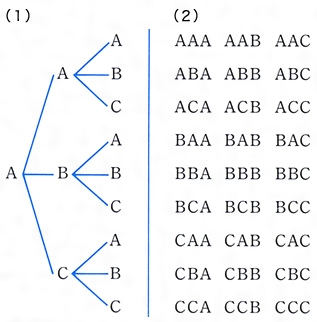
組合せとは いくつかのものからいくつかのものを取り出して並べることを順列と呼んでいました.ここでは,取り出したときの順序を考えない場合の数を考えてみましょう.そのような問題は組合せの問題と呼ばれています. 順列 $\rightarrow$ 順序を考慮 (区別)する.場合の数③ 組合せ 順列と組合せ 実は、ここまで学習してきた場合の数は、全て「順列」と呼ばれるものでした。このページでは「組合せ」について学習していきます。 では、順列と組合せはどこが違うのでしょう。 その違いは一言で言うならば、順番を気にするかしないかです。 ケタのよく「順列」と「組合せ」を間違って用いられている場合 ここで,5人から3人を選ぶ選び方(つまり組合せ)の数を仮に m とします。すると,5人から3人選出し並べる並べ方は,上のように1つの組に対し 3!




重複組み合わせ は2パターンを区別すればok



場合の数と確率の基礎を解説 受験に役立つ樹形図 数え上げのコツ Studyplus スタディプラス
前回 https//wwwyoutubecom/watch?v=FkOCL5MZ5wM 次回 https//wwwyoutubecom/watch?v=72cqwjJa5sMサブチャンネル とある男がゲームを具体的な場面における場合の数を,組合せを用いて求めることができるようにする。 (2) 観点別評価規準 具体的な場面における場合の数を,組合せを用いて求めることができる。表現・処理 (3) 準備物 ワークシート,画用紙,マグネットシート,ホワイトボードマーカー (4) 学習の展開 学習 組合せの定義 組合せ とは、 いくつかの異なるものから希望の数だけ選んだものや選ぶこと です。 このような場合、 選んだものの 並び は考慮されません 。 たとえば、A,B,CとB,A,Cは、並びが異なっていても 同じもの として扱います。 この点が、並ぶ順番が変わると別物として扱う順列




高校 数学a 場合の数24 組合せの計算 15分 Youtube




数学a 場合の数 組分け Youtube
この記事では,「A,B,Cの3文字から全部で7個選ぶ場合の数」のように,同じものがいくつかあってよい「重複組み合わせ」の考え方を説明します. 「重複組合せ」の問題設定としては 選ばれない色のボールがあっても良い場合 選ばれないボールがあってはC o m b i n a t i o n s (1) n C r = (n r) = n!組合せ数 nCr C o m b i n a t i o n s (1) n C r = (n r) = n!
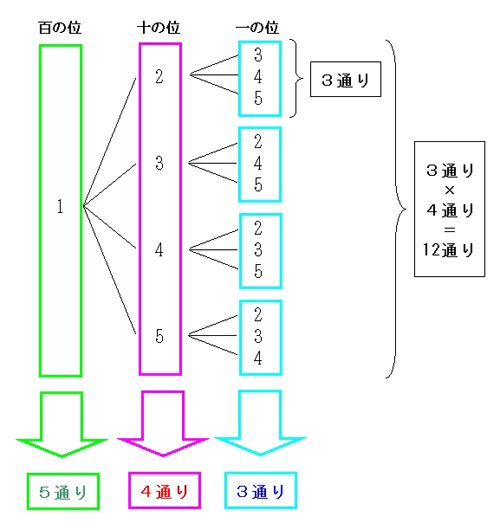



場合の数




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ
(2) n C r = n P r r!例えば、エクセルで順列や組み合わせなどの場合の数を求めるにはどのように対処するといいのか理解していますか。 ここでは、 エクセルで順列、組み合わせ数を算出する方法 について解説していきます。 ・エクセルで順列の計算を行う方法場合の数 ・エクセルでの重複順列の求め方 ・以前に学習した「男女を 一列に並べる 場合の数」では順列 n P r を使って数えたけど、「男女を 選ぶ(だけで並べない) 場合の数」だということに注意しよう。 「選ぶだけ並べない」 ときは、 組合せ n C r で計算することができたね。 男女を選びだすときの総数 の解法は次のポイントのよう
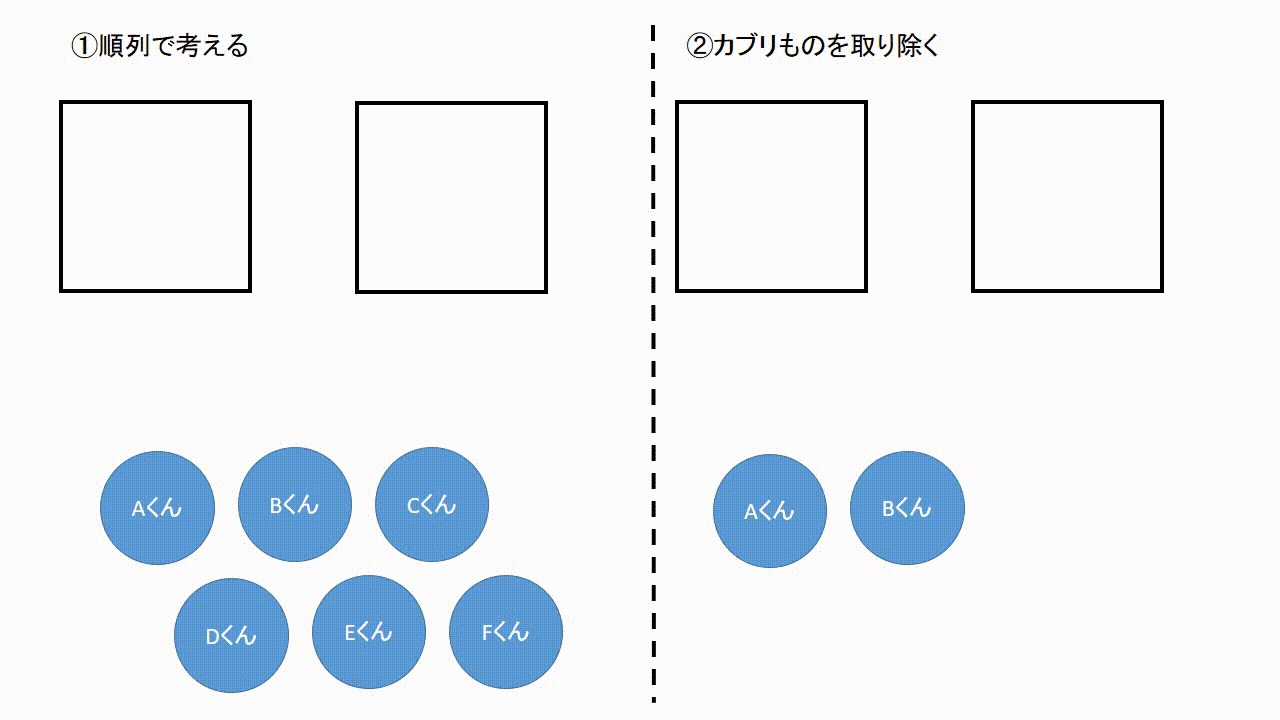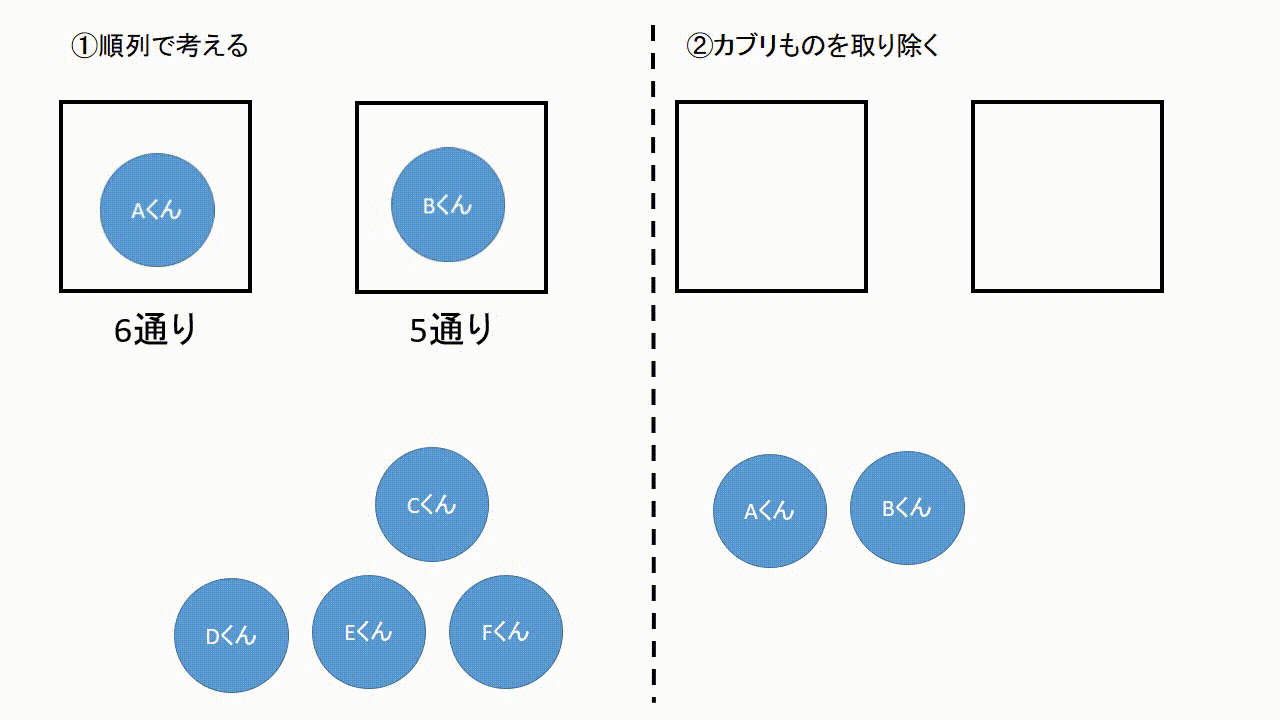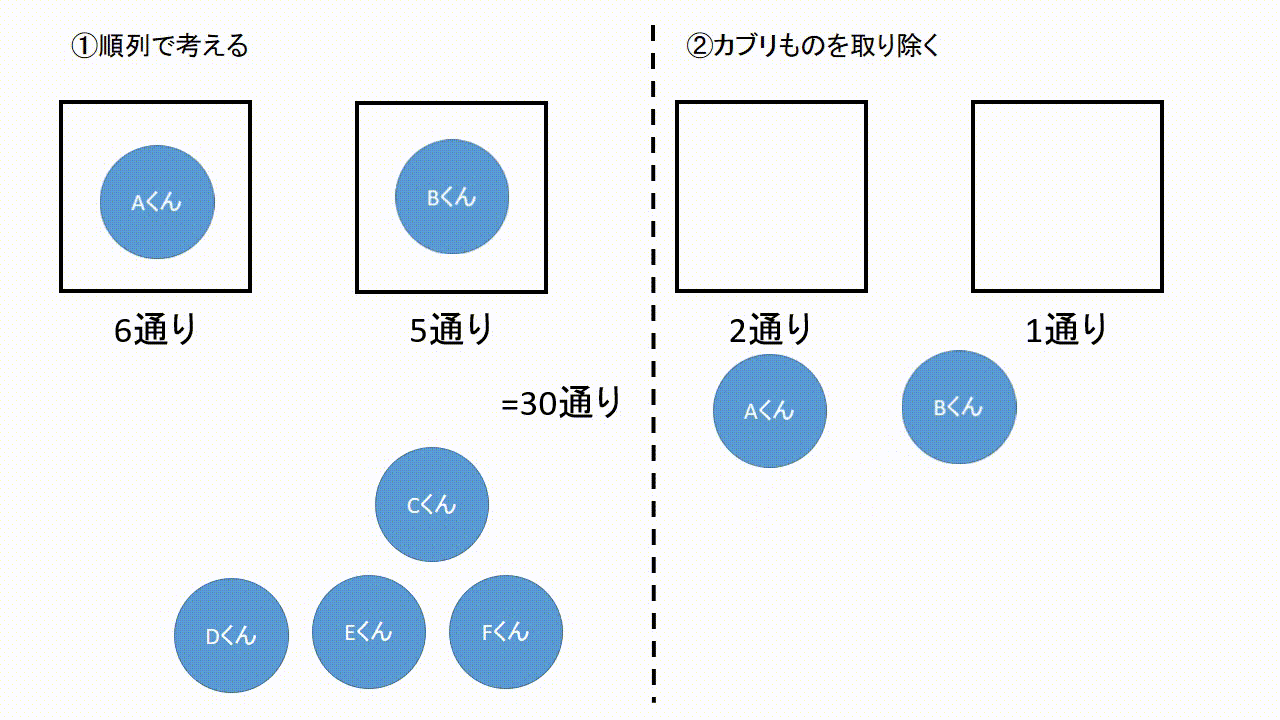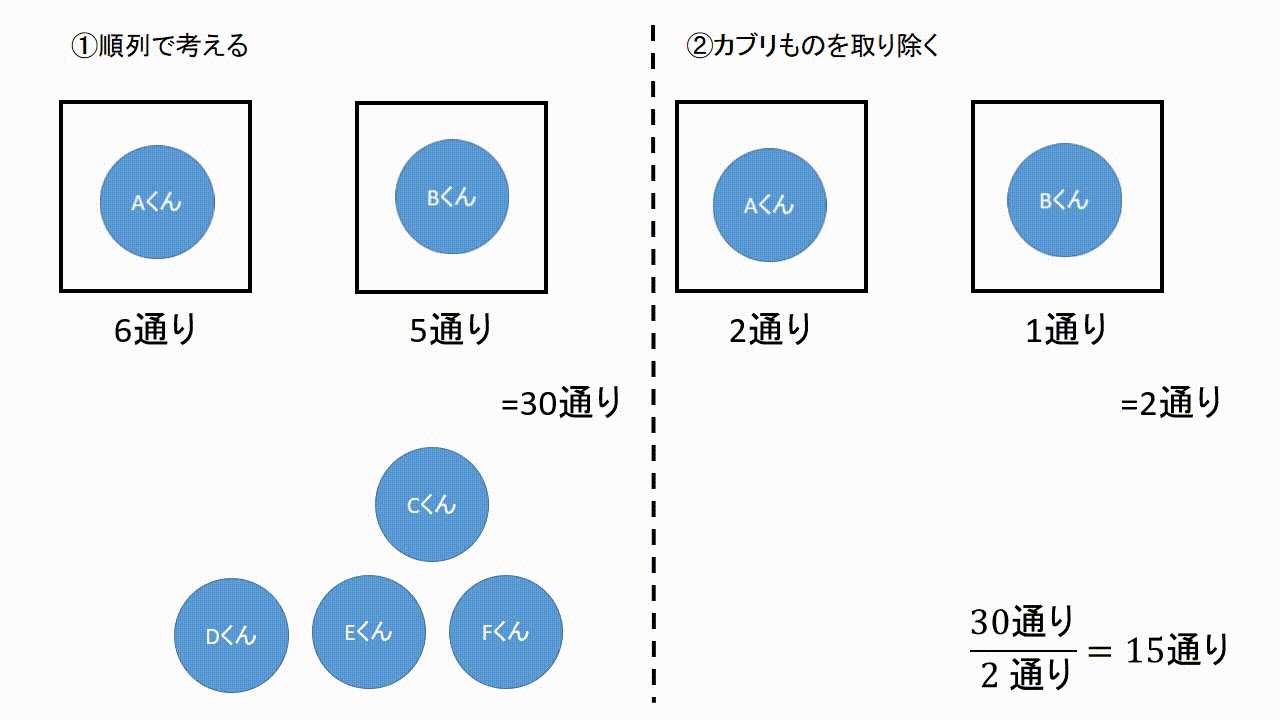



数学 確率を極めるには 場合の数 を極めろ




場合の数を考えてみる その2 組合せ 妹z会中学受験コース4年
授業実践記録(数学) 1. はじめに 中学2年生の「場合の数」についての授業実践報告をしたいと思います。 「場合の数」で苦労する生徒たちも多いと思います。 本来ならば高校1年生で習得する「集合論」を理解した上で「場合の数」に入っていくこと COMBIN 組み合わせの数を求める 対応バージョン: 365 19 16 13 10 総数個の項目のなかから抜き取り数個を取り出したとき、何種類の組み合わせが可能であるかを求めます。 二項係数を求めることもできます。場合の数 数学A 場合の数「順列」と「組合せ」の 違いを例題付きで解説します じゅじゅ高校数学Aの「場合の数」では、「順列」や「組合せ」の問題が多数出てきます。 いろんな考え方があって、覚えるのも大変ですよね。 本記事を読めばわかる



場合の数の一般問題 京極一樹の数学塾




場合の数 順列 組合せ のブログ記事一覧 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
場合の数と確率の分野では、原則として「人」は何も書いていない場合は区別します。 一人一人が3 これは以前紹介した重複組合せそのままですね! 未だ読んでいない人は→「重複組合せを得意にするたった一つの考え方」をご覧下さい! 従って、丸仕切り法の考え方を使って、6つの丸場合の数大中小3つのサイコロを投げるとき何通り?奇数、偶数?4の倍数? 場合の数と確率 53 数学a組み分けの場合の数の求め方・考え方をイチから解説! 中学生向け! 数スタの逆転メルマガ講座 無料のメルマガ講座はこちら! ホーム 中学1年生数学記事一覧 中学2年生



組み分け 部屋分け 問題全8パターンと解き方 数a 場合の数確率 そうちゃ S 図解英数ゼミナール



Q Tbn And9gcqhmwwpfbuiyilxexfg61ffig4wlm2aeogxhjnko A5xk1ftzru Usqp Cau



組み合わせを書き出す 中学受験算数 場合の数 どう解く 中学受験算数




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら




重複順列と重複組合せ 感じる科学 味わう数学




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら



場合の数 組合せについて 日々是鍛錬 ひびこれたんれん




高校数学a 組合せの活用1 点を結ぶ 例題編 映像授業のtry It トライイット



順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




高校数学a Npr と Ncr の使い分け 練習編 映像授業のtry It トライイット




6年算数場合の数 1 教え方のポイント




高校数学a 組合せの活用4 少なくとも 映像授業のtry It トライイット




場合の数17 数の順列1 怜悧玲瓏 高校数学を天空から俯瞰する




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート




高校数学a 組合せの活用4 少なくとも 練習編 映像授業のtry It トライイット




場合の数 無料で使える中学学習プリント



重複組み合わせは絵を描けば理解できる イラストで解説 理数白書




高校数学a 組合せの計算1 Ncr 練習編 映像授業のtry It トライイット



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




高校数学a 組合せとは 映像授業のtry It トライイット




公式集 4 3 場合の数 組合せ 分ける 編 コメディカル受験対策講座




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート




高校数学無料問題集 数a 第1章 場合の数と確率 組合せ 桝 ます Note




場合の数 並べる と 選ぶ の計算方法の違い




場合の数39 重複組合せで楽になるいいかえ 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学a 場合の数 組合せ頻出 男女を選ぶ問題 高校生 数学のノート Clear



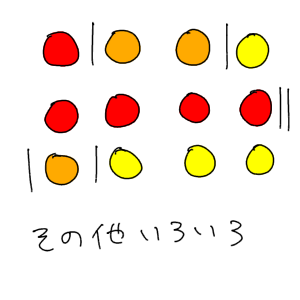
場合の数 算数用語集
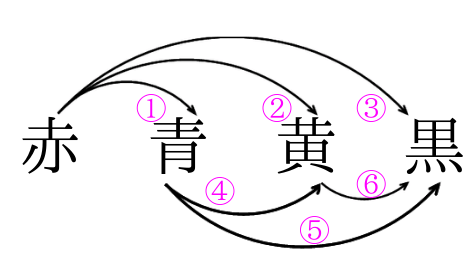



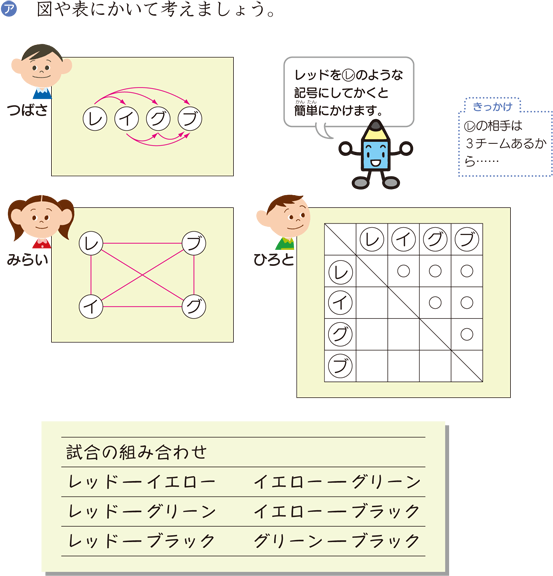
小学校で扱う場合の数の組み合わせの考え方 みけねこ小学校




算数 場合の数の解き方は 問題別に考え方を解説 数スタ




数学a 重複組み合わせ問題 場合の数 チャート 実践例題集 自宅でできる受験対策ショップ ワカルー Wakaru
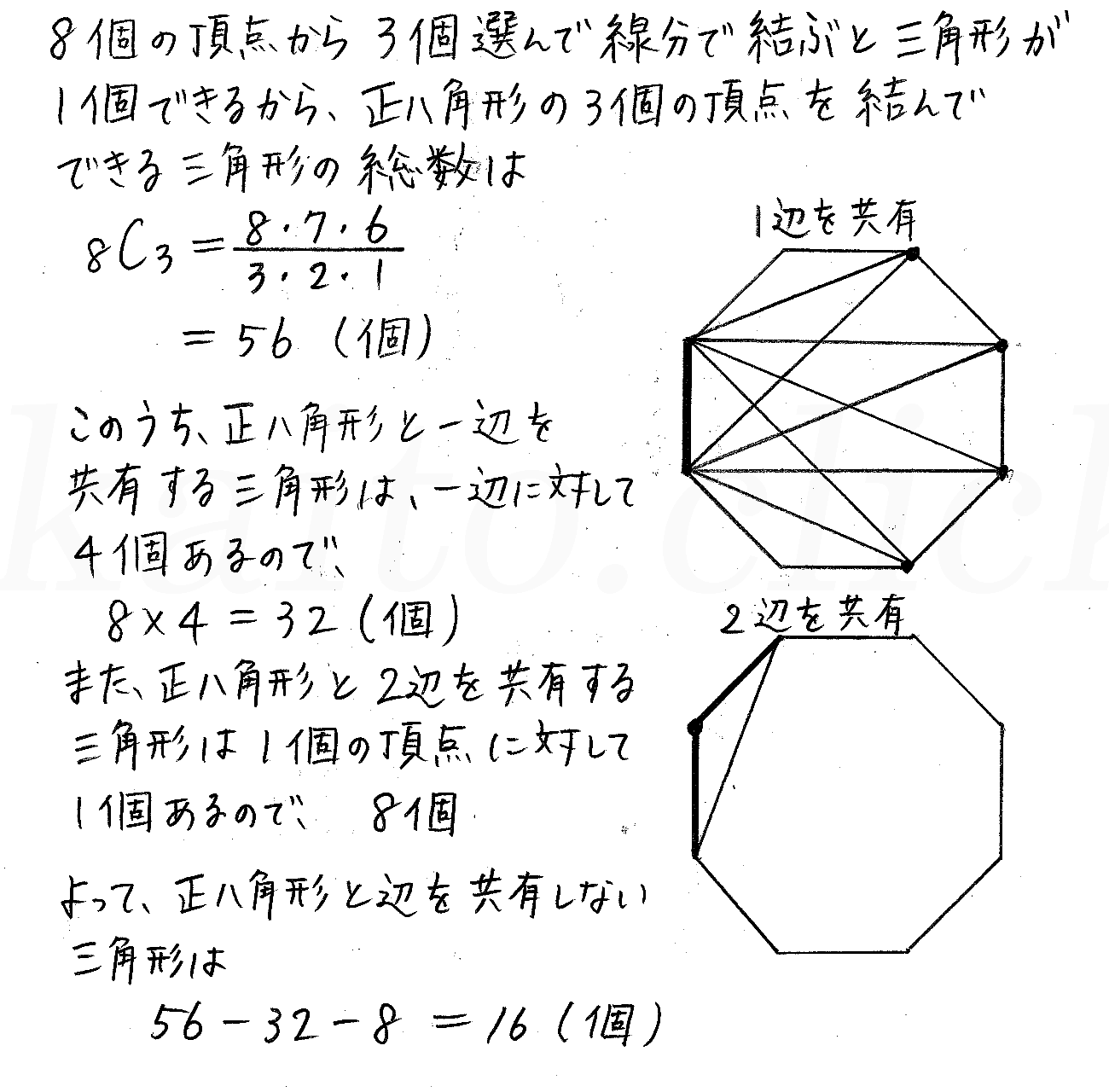



改訂版 4プロセス数学a P118 4 組合せ




高校数学 数a 17 組合せ 道順編 Youtube



数学言語としての場合の数の求め方



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾




順列と組み合わせの違いとは そしてそれぞれの意味を0から解説




場合の数38 重複組合せの導入3 怜悧玲瓏 高校数学を天空から俯瞰する



場合の数 算数用語集



組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける



場合の数 確率の総合案内 定理 公式の総まとめと復習 そうちゃ S 図解英数ゼミナール




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




場合の数 組み合わせの計算方法について 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開



順列 組合せの場合の数と確率の例題 Of 京極一樹の数学塾




高校数学a 組分け問題全パターン 受験の月




高校数a 場合の数 Cの計算方法 オンライン無料塾 ターンナップ Youtube




重複組合せはなぜ仕切りを使うの 整数解の個数を求める問題で鍛えよう 遊ぶ数学




数学a 場合の数 組み合わせの総数 Youtube



区別がない組分け 数学 苦手解決q A 進研ゼミ高校講座




苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ



3




場合の数 順列 と 組合せ の 違いを例題付きで解説します




場合の数 重複組合せ と 重複順列 の違いをわかりやすく解説します




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



数学a 重複組み合わせ問題 場合の数 チャート 実践例題集 自宅でできる受験対策ショップ ワカルー Wakaru



場合の数とは コトバンク




場合の数19 円順列と数珠順列 怜悧玲瓏 高校数学を天空から俯瞰する




場合の数36 重複組合せの導入1 怜悧玲瓏 高校数学を天空から俯瞰する




場合の数 並べる と 選ぶ の計算方法の違い



場合の数 学び家 Com




場合の数 組合せについて 日々是鍛錬 ひびこれたんれん



1




スマホok 6年 並べ方と組み合わせ方 場合の数 並べ方を考えよう Youtube




これならわかる 図解 場合の数と確率 佐藤敏明 本 通販 Amazon




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




順列と組み合わせの公式とその違い 問題付き 理系ラボ




高校数学a 組合せの基本と順列との関係 Ncrの性質 受験の月




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




中学数学 場合の数




中学受験 算数確認チェック29 場合の数 順列 組み合わせ グランパは元塾長



場合の数 順列と組み合わせの違いと並べ方問題の解き方




高校数学a 重複組合せ Nhr 受験の月




場合の数 組合せについて 日々是鍛錬 ひびこれたんれん




場合の数 順列 組合せ 2020年度前期日程の神戸大学文系の入試より 身勝手な主張




苦手でも分かる 順列 P と組み合わせ C の使い分け 確率 ともよし塾 受験と科学の解説授業
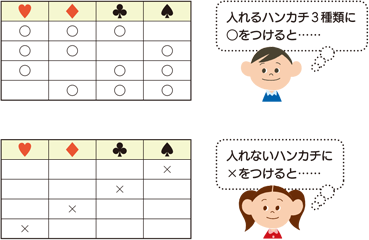



順列と組み合わせ 算数用語集




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生
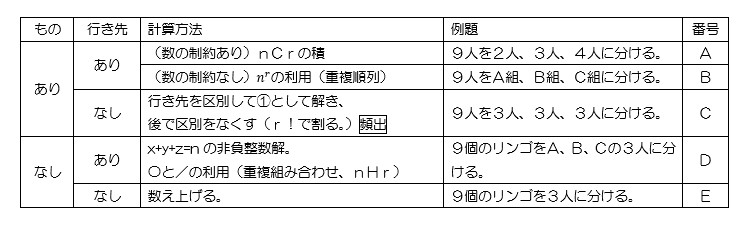



場合の数 確率を体系的に学ぼう 教科書でバラバラに登場するパターンを整理して把握しよう オンライン受講 東大に 完全 特化 東大合格 敬天塾




数学a 場合の数 順列の問題か 組み合わせの問題かの見分け方 坪田塾 公式youtubeチャンネル Youtube




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




場合の数 並べる と 選ぶ の計算方法の違い




確率の問題の解き方 場合の数 組み合わせ と確率 現役塾講師のわかりやすい中学数学の解き方




重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ




中学受験算数 これだけ 算数のカギ 場合の数 組み合わせの計算方法 Spi Youtube




場合の数38 重複組合せの導入3 怜悧玲瓏 高校数学を天空から俯瞰する
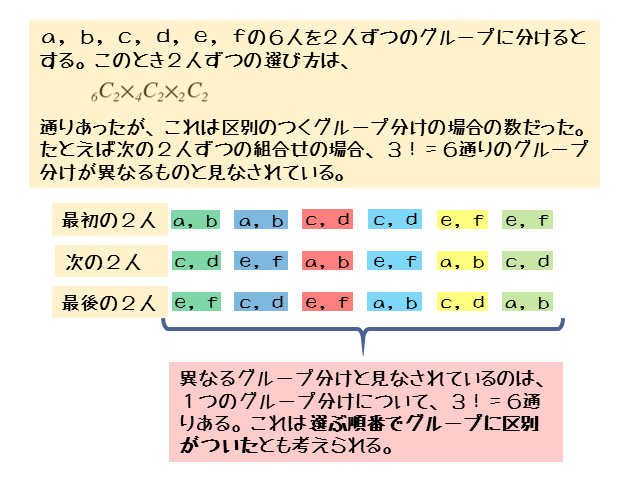



場合の数 グループ分けについて 日々是鍛錬 ひびこれたんれん




数探高校講座 数学a 場合の数と確率 5 組合せ 数学探究所
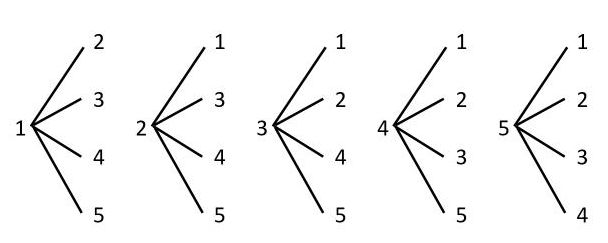



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ



0 件のコメント:
コメントを投稿