物理を勉強していると, 近似計算にでくわすことになる はじめのうちは, 「なんでこんなことしているのか?」「値がズレちゃうん 近似値じゃなくて確実な数字をです! お願いします! 数学 数学 √3984 の近似値の求め方教えてください! 数学 数学 ルート2から10までの覚え方を教えてください。 数学 平方根の値と近似値の問題 ①√23=152、√23=480 として、√0023の値を求めよ。 答えは0152 なのですが、求め方を教え 平方根(ルート)の近似値の求め方 √2≒141 というのは聞いたことがありますか? 平方根を、近い大きさの数である「近似値」で表せ、という問題はよく出題されます。ここではこの、「平方根の近似値」について説明します。 覚えるべき近似値 近似値の求め方はあとで解説しますが、√2

平方根で近似値の応用問題です はどうやって解きますか Clear
近似値とは ルート
近似値とは ルート- ニュートン法を用いると、√2の値やsin(x)=05になるようなxの値など近似的に求めることができます ニュートン法の考え方 ニュートン法では、以下の考え方に基づいて計算が行われます f(x) = 0になるような値xを探す時、ある値x1における接線の切片x2は、元の値x1より真の値xに近くなルートの近似値の求め方 a \sqrt{a} a の近似値の求め方の概要: x 2 ≒ a x^2≒a x 2 ≒ a となりそうな簡単な x x x を探す。 ルート2の近似値は、面積が4の正方形から、 面積が2の正方形を作図して分かりました。 同様にルート3の近似値を面積3の正方形を作図して一辺を計ろうとしましたが




ルートの近似値を計算する素朴な方法とコツ 高校数学の美しい物語
ルート11からルート30までの近似値 有名な語呂はありません、覚える必要もありません! ルート11:$$ ルート12:$$ ルート13:$$ ルート14:$$ ルート15:$$ ルート16:$4$ ルート17:$$ ルート18:$$ ルート19:$435$ ルート:$$ ルート21:$$ ルート22:$でより良い近似値が得られるのに,分数ではそうはいかないではないか,というように。 しかしながら本稿では,1と2の間をできるだけ粗く区切って,それでもよい近似値を得るというこ とを考えましょう。という近似値は,1と2の間を1億等分した,いや,分数で表せば約分 できる ¡ 平方根の大小をくらべる問題とか、ルートの近似値 を 244っていうのはあくまで大まかな値。ルート6は無理数だから無限にランダムに桁数が続いていくはずだ。 244を実際に電卓で2回かけてみるといいよ。6に近い値が算出されるはず みかん より 18年3月13日 107 PM √n=196 が384になるのが
のレビュー 近似値 ルート 求め方 アルバム ルート Engage このサイトについて 近似値 ルート 求め方 記事 (21) See 近似値 ルート 求め方 アルバムしかしまた見ますルート 近似値 求め方 電卓 に加えて Celleforandringer I Livmorhalsen Behandling より詳しい情報物理では非常に小さい値を無視する近似が行われます いつ近似できるのかと近似の方法について議論します ホーム 物理の周辺 近似式 近似式 本論; ルート1 5の近似値 同じように、「5」「√」と押すと、「」と表示され√5の大体の値が求まります。 この大体の値を近似値と呼んでいます。この値はどうやって求まるのでしょうか。 ここでは、いくつかの求め方を考えてみましょう。 近似曲線をダブルクリックすることでも
ある数の近似値といえば,小数で表すのが普通であるが,まれに近似値を分数で表すことがある. 例えば,円周率 π=の近似値として,昔から , という分数による近似値が知られている. この分数近似はどうやって得られるのであろうか. まずを, と表すことを考える(νはルート2を求める 中3で初めて平方根を習うとき,$\sqrt{2}=\cdots$を求めるのに, $141$ まで。次の $1414$ なんて電卓がないとやる気が起こりません。本当に $\sqrt{2}$ の値を深く求めたいのであれば,やり方を変えた方がよさそうです。 図形から求める (中3) 直角をはさむ辺の長3の平方根(さんのへいほうこん)は、平方して 3 になる実数である。 正のものと負のものの2つがある。正の平方根は と書き、「ルート3」と読む。その小数表示は 1735 677




平方根 式の値 求め方はどうやる 問題を使って徹底解説 数スタ



画像 ルート 展開 近似 ハイキュー ネタバレ
02 ルートの近似値 続いて次の値の近似値を求めてみましょう! まず次のように変形します: すると x = 7/121 = を微小量 x とみなして、先ほど求めた近似式を用いることができます: 右辺を計算することで √128 の近似値が求まりました!2ルートの近似値について 数と式 \(\sqrt{2}\)や\(\sqrt{3}\)などの近似値が知りたい場面が多々ありますが すべてを覚えておくのは(私にとっては)難しく、 一般的によく語呂合わせで覚えることが多いです。 例えば ルート5 近似値, コラム『ルートの近似計算』 ルート(平方 平方根 (ルート) を覚えることをやめました。 どうも,ユキです。 平方根を自分で導くことが出来れば,覚える必要はありませんよね。 ということで,今回の話は,連分数を使って, 平方根の近似値を出す裏技 を公開します。




ニュートン法の例題 ルート3の近似値を与える方法 理数アラカルト
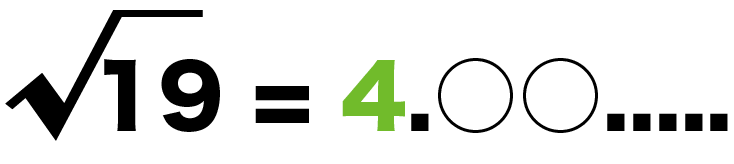



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく
近似値 きんじち approximate value 真の値すなわち正しい値そのものが算出できないとき,あるいは算出できてもそれほど精密な値を必要としない場合に,その代りとして使用される,真の値に近い数値のことを,近似値という。 たとえば は円周率 π の近似値,2718は自然対数の底 e の近似13 近似と極限 上の2つの例の数値計算により、与えられた点x = a(112 節の場合a =1、122 節の 場合a =2)の近くでの1次近似の誤差項の絶対値は、xがaに近いときxaの値と比べ て小さく、x がa に近ければ近いほどx a の値と比べてより(桁違いに)小さいことが 一般化二項定理を使うことでルートなどを近似できます: ルートの近似公式(一次近似) x x x が十分 0 0 0 に近いとき 1 x \sqrt{1x} 1 x は 1 x 2 1\dfrac{x}{2} 1 2 x で近似できる。 高校物理でもよく使う近似式です。背後には一般化二項定理(テイラー展開)があったのです! 例1 101 \sqrt{101} 1



関数電卓でルートxの近似値を出してくれる方法を教えてください ル Yahoo 知恵袋



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく
ルートの近似計算 コラム 「ルートの近似計算」 (改訂) 2 なる M を見つける訳ですが、 一般に M は整数とはならないため、整数 α 0, b を用いて A = α 0 2 ± b ( α 0 2 は平方因子、±b は調整項) ・・・① と、A をまず平方表現します。(α 0 は √A の第0近似値) ここで、調整項 ±b は A と α 0 2 とのπ の近似値 このページでは過去発表された円周率の近似値を表す数式を紹介する。 元の表記方法(の日本語訳)をそのままを使うと(特に古い文献で) 円周率を求めた記述ではないというような解釈ができるが ここでは π = π = の形に解釈したものを関数の近似とTaylor 展開 微分係数と接線の方程式 実数x の関数f(x) のx0 における微分係数f′(x 0) の定義は次の様に書き換えることが出来る。 lim x→x0 f(x)−f(x0) x−x0 −f′(x 0) = 0 つまりf(x) = f(x0)f′(x0)(x−x0)R(x) とおくと lim x→x0 R(x) x−x0 = 0 このことは を の近くで一次関数 で近似す




ルート2を連分数の極限として求めようとしたら行列が出てきた 前編 しいたげられたしいたけ




中3数学 平方根の近似値の問題です Clear
根号(ルート)の中の値を簡単にしてしてくれるプログラムです 2乗根、つまり普通の根号専用です 入力値は2以上100,000,000(1億)未満の自然数に限ります、まあ2や3は素数なので無意味ですが 結果に根号を含む場合は、ちゃんと根号を含めて表示します近似値の求め方が分かりません」 平方根の √a/b ( ルート の中に 、分数「b 分の a」が入っています) 分母、分子の両方に√ = √a ÷ √b (「分子 ÷ 分母」の割り算) この3行は、それぞれ イコールでつなぐことができます。 ご質問の問題は、 このルールを使いますよ! では、ご質問 ルート19万円ほしい っていわれてもピンとこないよね??笑 高いのか低いのか検討もつかん。 今日はそんな事態に備えて、 平方根のだいたいの値の求め方を勉強していこう。 この「だいたいの値」のことを、 数学では「 近似値 」とよんでいるんだ。 3




中学数学 平方根 整数になる自然数n の簡単なやり方 丁寧な解説 スタディーランナップ




ルート3の近似値の求め方4パターン 数学の星
What follows are the first 1 million digits of the square root of 2 Actually there are slightly more than 1M digits here These digits were computed by Robert Nemiroff (George Mason University and NASA Goddard Space Flight Center) and checked byReview (Approximate calculation by tangent line) Example sin59 の近似値を1 次近似で求めてみる. y = sin x のx = π/3 における接線l は l y = 1 2 x √ 3 2 − π 6 なので,x ≒ π/3 ならば sin x ≒ 1 2 x √ 3 2 − π 6 が成り立つ.そこで,x = 59 = 59π/180 とすれば sin59 ≒ √ 平方根はこれで完璧! 平方根の定義からルートの計算、近似値の問題の解き方まで 平方根という分野は中学三年生にとっての鬼門です。 ただ、これがなぜ中学生にとって難しいとされるのかという点については、少しだけ誤解があるようです



中3 平方根10 近似値 中学数学の勉強に




中3数学 平方根の近似値の問題です Clear
先ごろ、中村さんの「ルート を Aの平方根の第0近似値を 0 n a n)/2 により求めます。この初期値(第0近似値)の選び方により、収束の早さは異なりますが、この近似法はかな ルート23 のような 以上の手順を踏むと、\(\sqrt{23}=\cdots\) や \(\sqrt{53}=\cdots\) などの近似値を筆算することができます。 Tooda Yuuto 「計算ツールはどうやって平方根を求めているのか?」の考え方の参考として、ぜひ一度筆算を試してみてください。 >>関連記事:平方根√




中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく



中学数学 平方根



平方根の活用 式の値と近似値の求め方 教遊者
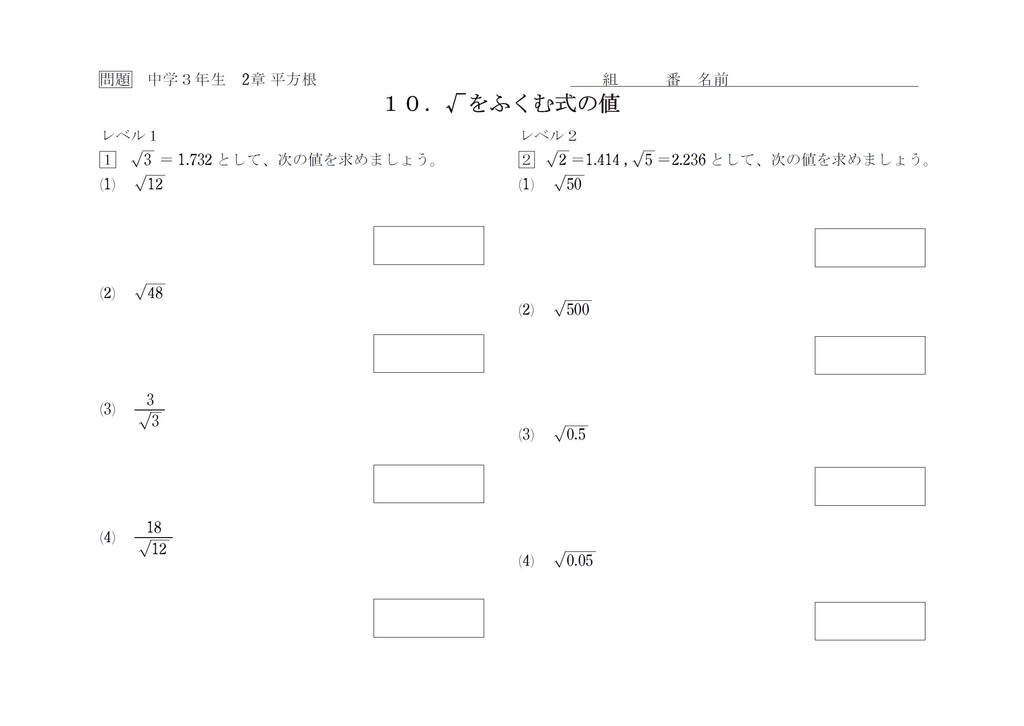



中3 平方根10 近似値 中学数学の勉強に




ルートの近似値の求め方 中3数学 Youtube



電卓でルート 平方根 を計算する方法
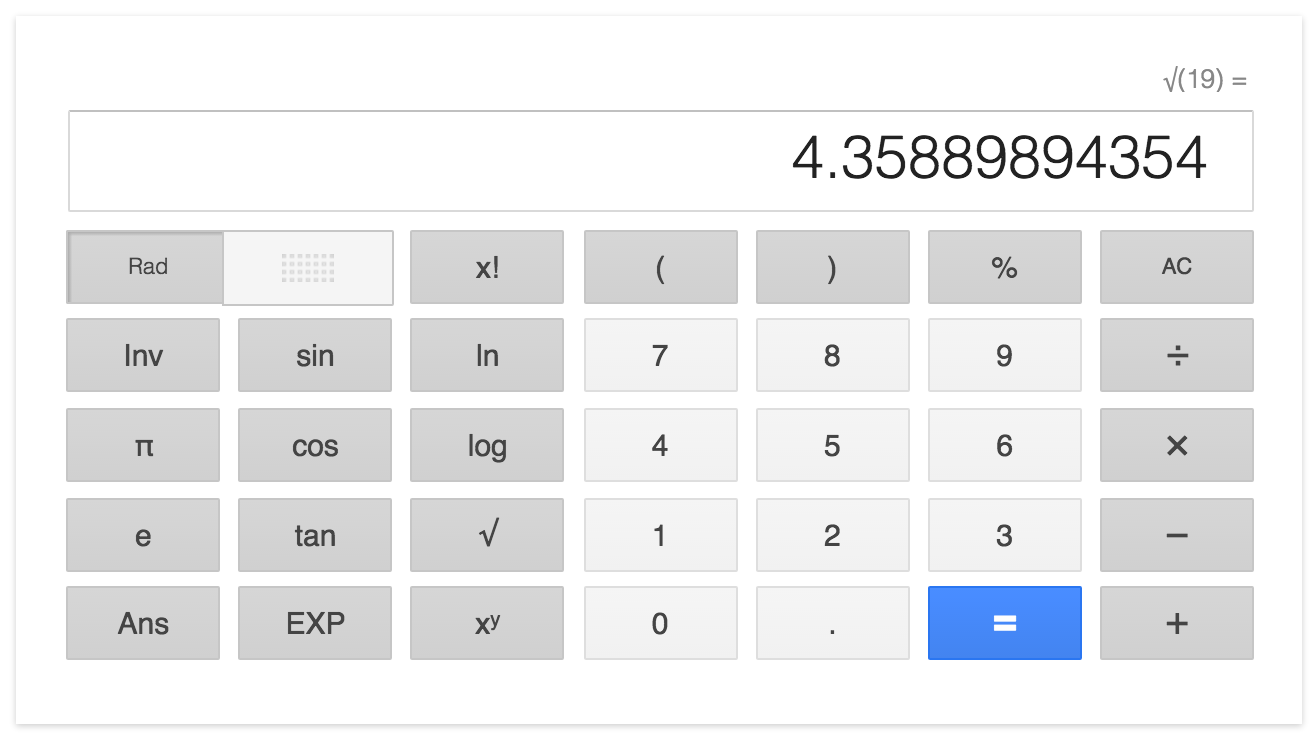



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく



第2章10平方根 平方根の近似値 フロントエンドなブログ




中学校数学 3年生 数量 平方根 Wikibooks




中1 数学 近似値と有効数字 中学生 数学のノート Clear




中3数学 平方根の近似値 映像授業のtry It トライイット
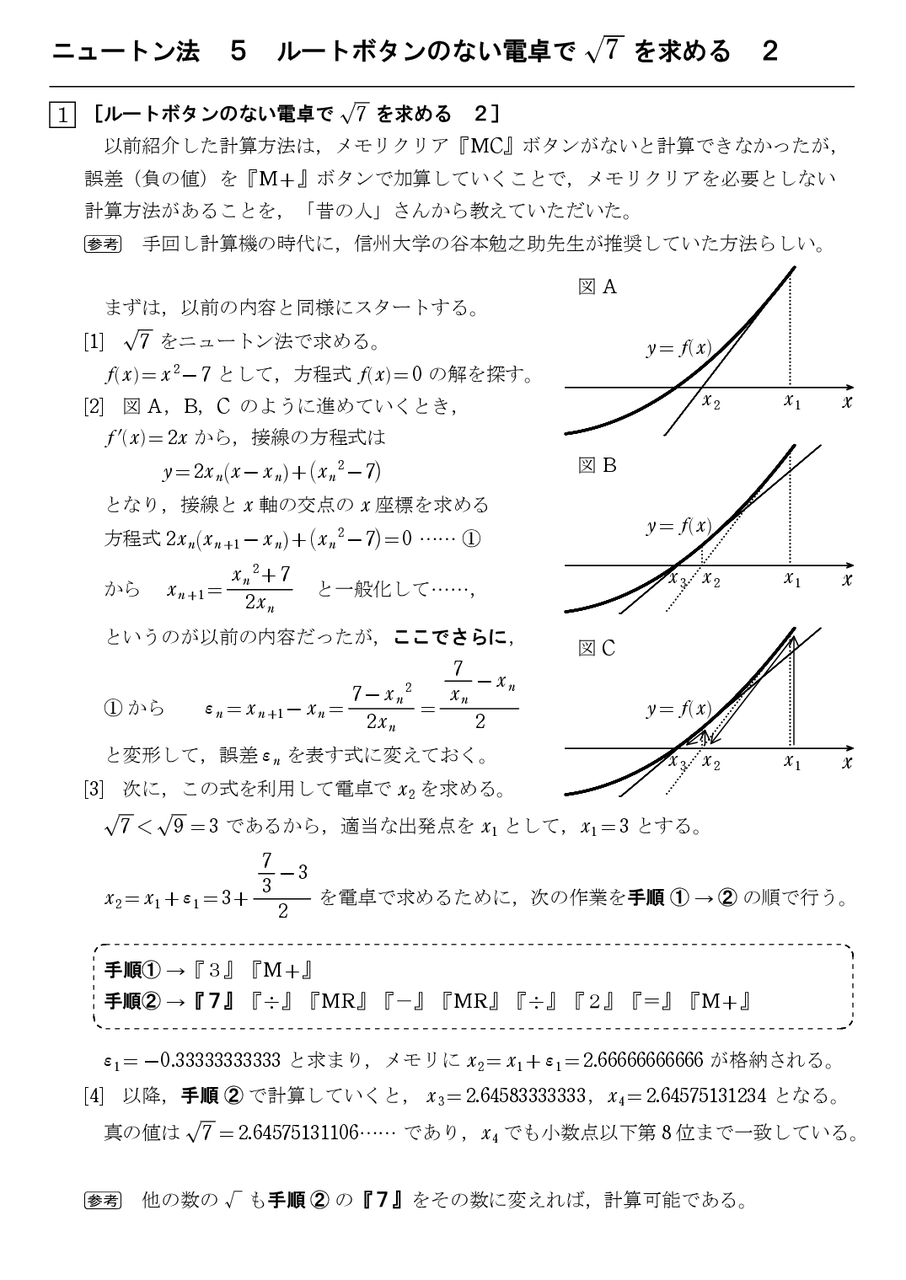



ニュートン法 5 ルートボタンのない電卓で平方根を求める方法 2 怜悧玲瓏 高校数学を天空から俯瞰する



1次の近似値を用いて次の数の近似値を求めよ ただしp 3 14ル Yahoo 知恵袋




中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく



平方根の手計算による解法 タックの庭仕事 黄昏人生残日録



画像 ルート 展開 近似 ハイキュー ネタバレ




2 1 414の近似値を使って平方根の近似値を求める 中3数学 平方根 Youtube




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




中3数学 近似値を使う計算 例題編 映像授業のtry It トライイット
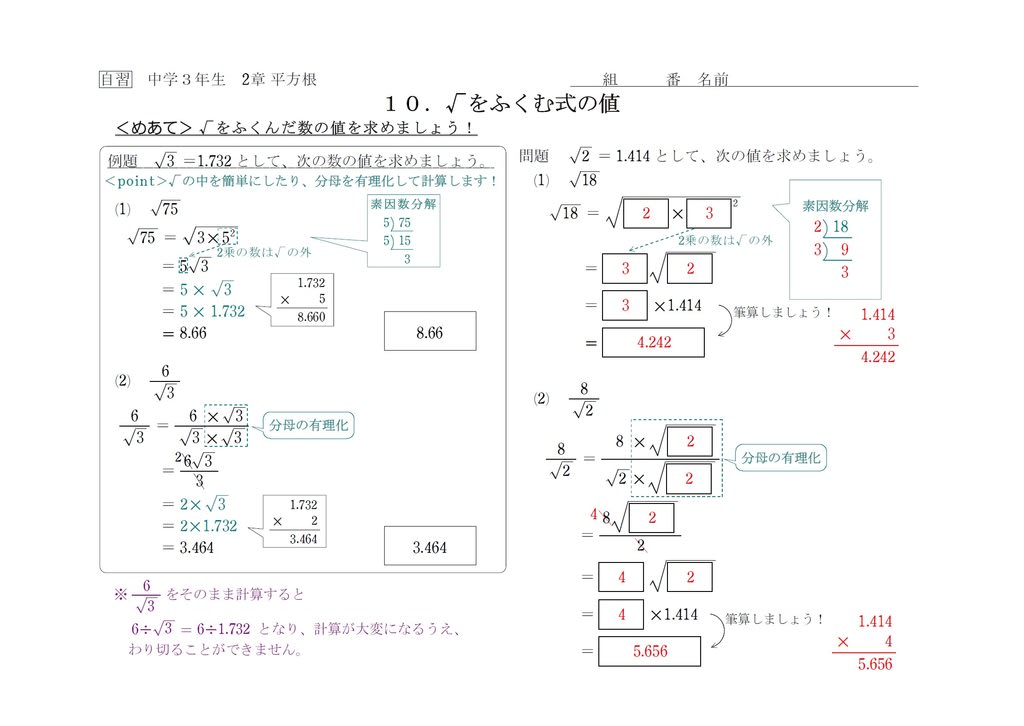



中3自習 平方根5 近似値 中学数学の勉強に



H Kinji



3 732 30 477とするとき 次の近似値を求め Yahoo 知恵袋




裏技公開 11のような平方根を速く求める方法 連分数使います Cupuasu クプアス




中3 数学 平方根6 ルートの近似値 4分 Youtube




中学数学3年 平方根とその近似値 大小 有理数と無理数 受験の月
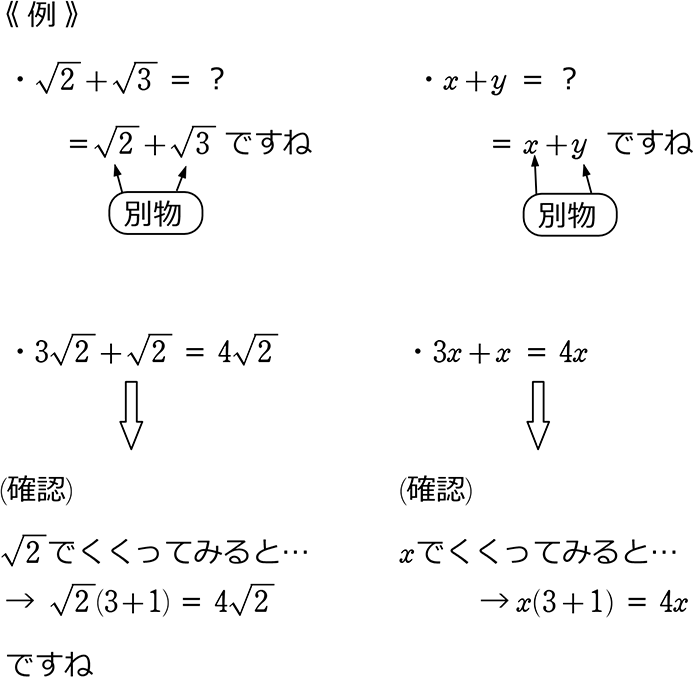



中学数学 平方根




裏技公開 11のような平方根を速く求める方法 連分数使います Cupuasu クプアス




中3数学 近似値を使う計算 練習編 映像授業のtry It トライイット




近似値 ルート8



1




無料 中3数学 発展 応用問題 問題プリント 314 平方根6 いろいろな計算1




ルートの近似値を計算する素朴な方法とコツ 高校数学の美しい物語




平方根の近似値 無料で使える中学学習プリント




ルートの近似値を計算する素朴な方法とコツ 高校数学の美しい物語
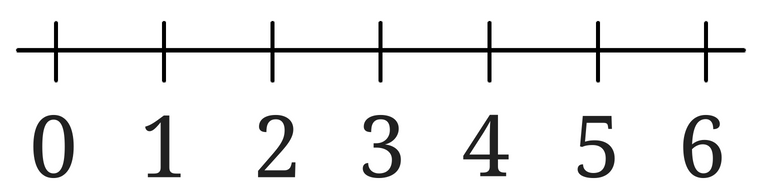



平方根の近似値を求めるにはどんな考え方をするの 語呂合わせを使った覚え方は さびねこ中学校




ルートの近似値の求め方 不等式を使って大小比較 趣味の大学数学




中3 ルートの近似値の求め方をイチから解説 Youtube




中1 数学 中1 近似値 Youtube




平方根の活用 式の値と近似値の求め方 教遊者



君はまだ テイラー展開の楽しさを知らない ルートの近似値 右螺子 理系大学院生 Note




平方根で近似値の応用問題です はどうやって解きますか Clear




平方根はこれで完璧 平方根の定義からルートの計算 近似値の問題の解き方まで




平方根とは コトバンク




数学 近似式まとめ 各種公式 求め方 理系ラボ



3




ルート2を連分数の極限として求めようとしたら行列が出てきた 前編 しいたげられたしいたけ



中3 根号の近似値 の教え方 塾講師 数学マンは踊る




2の平方根 Wikipedia




中3 平方根10 近似値 中学数学の勉強に




中3 数学 無料学習プリント教材




平方根の近似値 無料で使える中学学習プリント



Www1 Iwate School Jp Action Common Download Main Upload Id 1384




ルート2 ルート3 ルート5の覚え方など 高校数学の美しい物語




ルート5ほかの近似値 三平方の定理 よし坊のブログ




平方根のおよその値 近似値




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく




中学数学 平方根 のコツ 平方根の近似値 式の値




ルート3の近似値 よし坊のブログ



この写真の平方根表を使います 7 2が少数第3位を四捨五入すると 2 Yahoo 知恵袋




中3数学 平方根の近似値 Youtube



近似値 アプラクシマトリー クイズ ケペル先生のブログ



1



Studydoctor ルートの近似値の求め方 中3数学 Studydoctor




中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




6 の正しい近似値を教えてください 左がネット 右が教科書 です Clear



ルートを開こう




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ



中3数学です 次の数の近似値を 平方根表を使って 小数第3位ま Yahoo 知恵袋




ルート3の近似値の求め方4パターン 数学の星
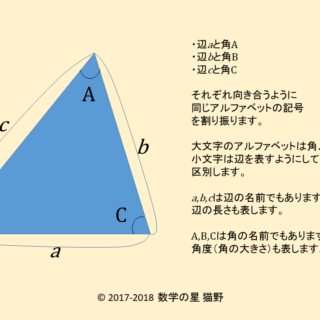



ルート3の近似値の求め方4パターン 数学の星



しょうちゃん 公式ブログ 開平法 ルートの近似値の求め方 Powered By Line



1




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




近似値と有効数字の求め方とは どちらも情報の 度が大事 遊ぶ数学




平方根 近似値を求める 苦手な数学を簡単に
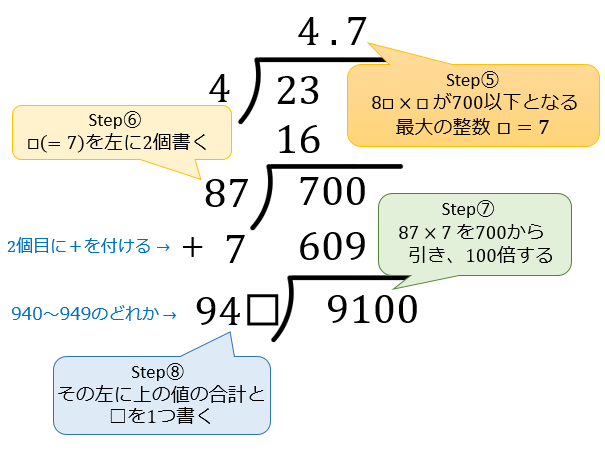



ルート2ルート3ルート5ルート7のゴロ合わせ 素数の平方根の筆算の仕方 アタリマエ




6 の正しい近似値を教えてください 左がネット 右が教科書 です Clear




計算機プログラムの構造と解釈 第二版



中1です この近似値を教えて下さい 塾には行っていないので自分で一時間 Yahoo 知恵袋



平方根まとめ




中3数学 平方根 ルートの値を語呂合わせ 覚え方まとめ 数スタ




ニュートン法によってルート 円周率の近似値を求めてみよう 趣味の大学数学




平方根の活用 式の値と近似値の求め方 教遊者
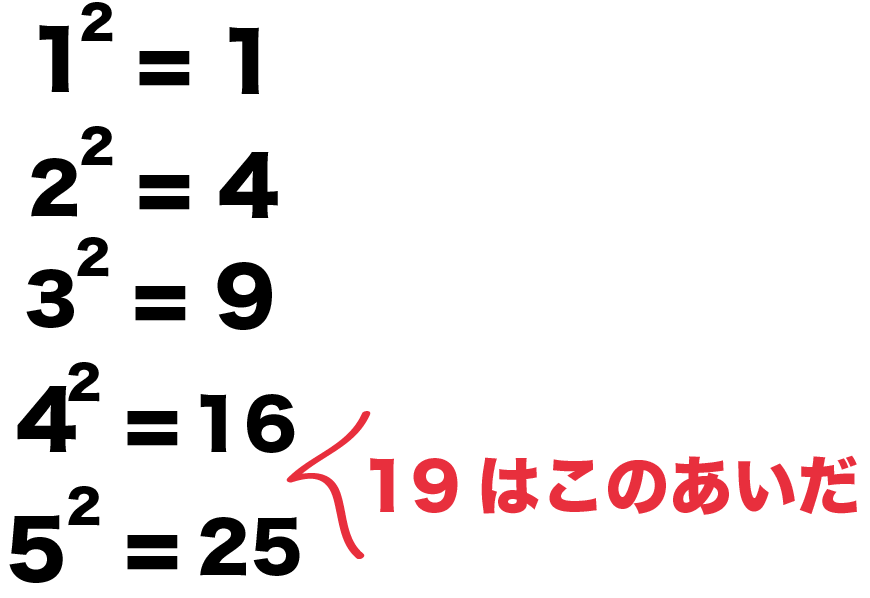



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




高校数学 ペル方程式x Dy 1で定められた数列の極限と平方根の近似値 受験の月




勝手に北辰テスト対策 数学 平方根 蒼進塾 そうしんじゅく さいたま市 真剣に努力する姿勢を育む




平方根 ルートの計算



Python Tkinterで平方根の近似解を求めるguiツール G6no3 Blog
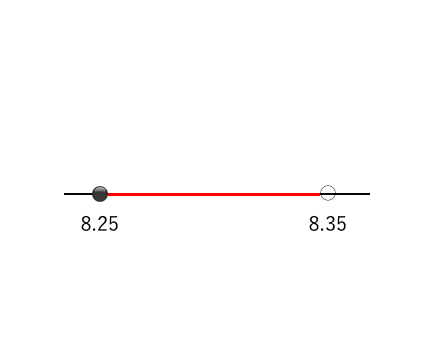



近似値の問題 苦手な数学を簡単に




高校数学 近似値 平方根 円周率 常用対数 自然対数の底 のゴロ合わせ 受験の月



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




ルート2の近似値を知る その1 よし坊のブログ



0 件のコメント:
コメントを投稿